Document

title: 计算机系统基础:浮点数的表示 date: 2022-10-07 23:23:41 tags: CSAPP

前言

大二的时候学习过这部分知识,现在也只剩下模糊的印象了,隐约记得做题的时候要算来算去好不麻烦.

为了速成看了一些技术博客,但总感觉走马观花,绝知此事还是要躬行,故留此文以便日后忘记之际重温.

本文主要参考深入理解计算机系统第三版书籍中对于该部分的描述,并且例举一些书中的习题以加深印象,以及CSAPP的Data Lab实验对于浮点数的函数实现

二进制小数

对于一个十进制的数 12371892398, 这个表达式描述的数被定义为

$$ d = \sum\limits_{i=0}^n10^i\times d_i $$

如果我们考虑小数点 . , 那么左边的权是正幂,右边是负幂,例如 $12.34$ 表示的数字是 $1\times 10^1 + 2\times 10^0 + 3\times 10^{-1} + 4\times 10^{-2}=12\frac{34}{100}$

而对于二进制数,这个权就变为了2 ($d = \sum\limits_{i=0}^n2^i\times d_i$),所以对于 $101.11$来说这个值就是 $1\times 2^2 + 0\times 2^1+1\times 2^0+1\times 2^{-1}+1\times 2^{-2}=5\frac{3}{4}=5.75$

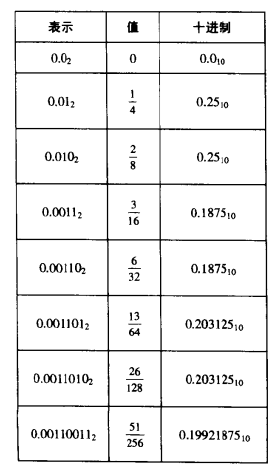
假定我们仅考虑有限长度的编码，那么十进制符号是不能准确地表达像 $\frac{1}{3}$ 和 $\frac{5}{7}$ 这样的数的。类似地，小数的二进制表示法只能表示那些能够被写成 $x\times 2^y$ 的数。其他的值只能够被近似地表示。例如，虽然加长二进制表示能够提高近似表示数'的精度，但是我们并不能把它准确地表示为一个二进制数:

IEEE 浮点数表示

像前一节中谈到的位置表示法不能很有效地表示非常大的数字。例如，表达式 $5\times 2^{100}$ 的表示是由 101后面跟随100个零的位模式组成的。相反地，我们希望通过给定x和y 的值，来表示形如 $x\times 2^y$ 的数。

IEEE浮点标准用 $V=(-1)^s\times M \times 2^E$ 的形式来表示一个数:

符号S 用来决定这个数是负数(s=1)还是正数(s=0),对于数值0的符号位解释作为特殊情况处理

有效数 M 是一个二进制小数,它的范围在 1~2-e 之间,或者在0-1-e之间

指数 E 是2的幂,可以是负数,它的作用是对浮点数加权

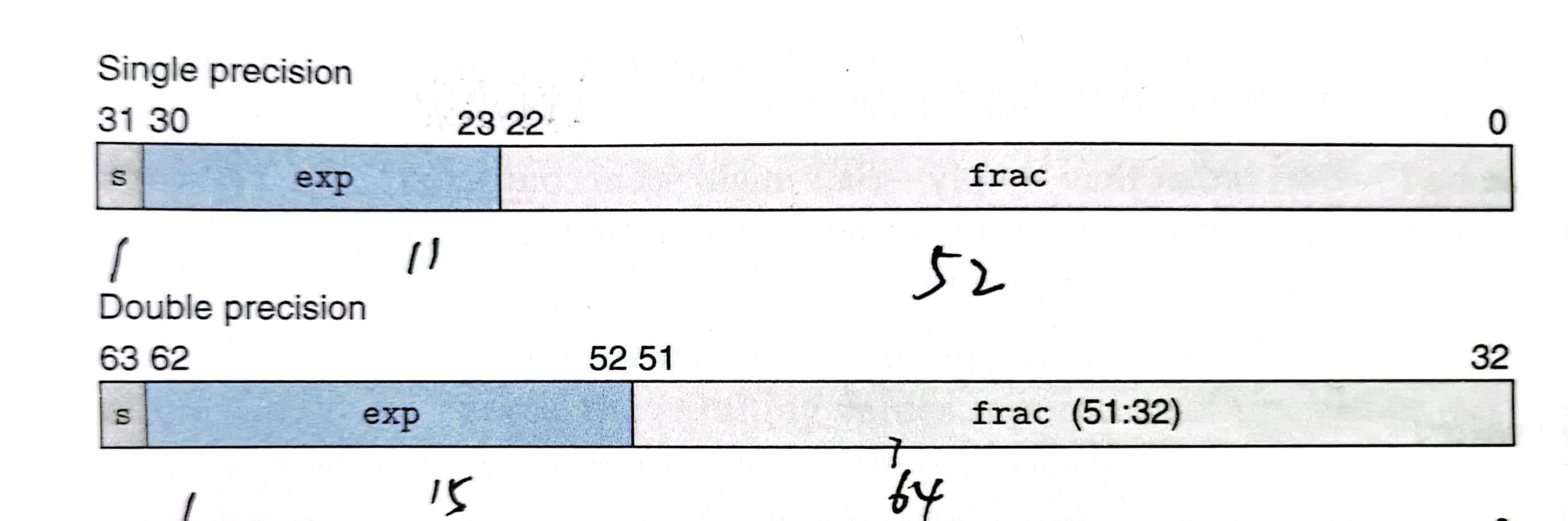
所以IEEE754标准规定了如下的三个域

s对应符号位,exp对应E指数位,frac则是对应有效数M

float 32位 : 1(s) + 8(exp) + 23(frac)

double 64位 : 1(s) + 11(exp) + 52(frac)

接下来按理来说应该讲到规格化和非规格化的部分,但是这部分记忆的内容有点复杂,大片的文字也比较容易劝退,所以我想直接上图,我们对着结果来反过来讲

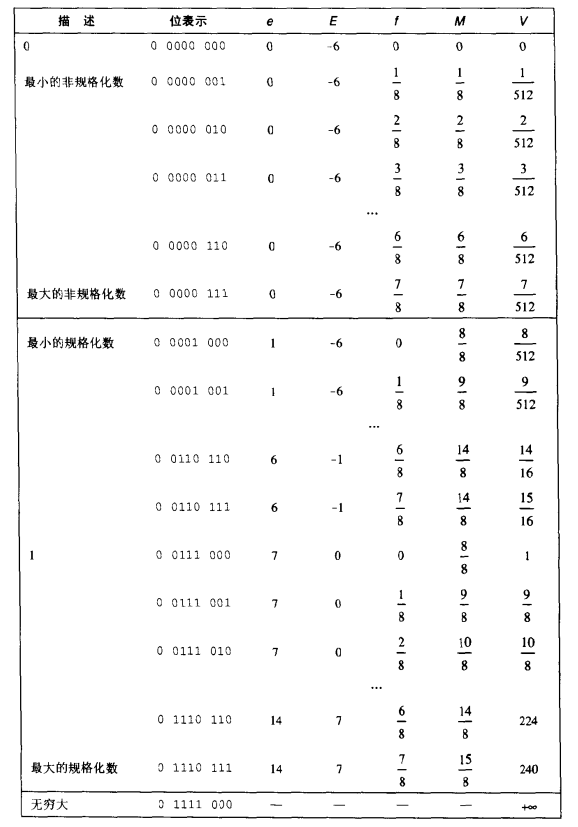
这是一个8位的浮点格式,格式为 1(s)+4(exp)+3(frac)

对于非规格化的数,即分割横线以上,他们的特点是(exp)的部分都是0,然后后面的(frac)部分在不断增加

规格化的则是这两部分01都有

最后的正无穷则是(exp)部分全为1,(frac)全为0

注意到上面有e E f M V五个字母,我们先观察一下他们和左面数据的对应关系,可以得出

e 是指数部分,和(exp)的二进制值相同

E 是指数,在非规格化的时候一直是-6,在规格化的情况下是e-7

f 是小数部分,在非规格化的时候和M相同,规格化的时候是 M-1

M 是有效数

V 是小数的值,根据之前的IEEE754的公式,可以得到 $V = 2^E\times f$

现在经过一个初步的分析我们已经可以看出一些关系了,但是还有一些疑问

e 和 E 有什么关系呢?

f 和 M 有什么关系呢? 这两个值又是怎么算出来的呢?

这里的分隔线提到的非规格化和规格化是什么意思呢? 又为什么要这么做呢?

对于第一个问题 : e 和 E 有什么关系呢?

之前提及的这个8位的浮点格式为 1(s)+4(exp)+3(frac),这里一个非常重要的概念是偏置项(Bias),这个数的计算方法是 $2^{exp-1}-1$ ,即 $2^{4-1}-1=7$

对于非规格化, E = 1-Bias = -6

对于规格化, E = e-Bias

这样我们利用了一个Bias就可以实现指数E的正负,既可以表示一个相对大的数,也可以表示一个趋近于0的数

对于第二个问题 : f 和 M 有什么关系呢? 这两个值又是怎么算出来的呢?

f的分子部分很容易看出是剩下的 (frac) 的二进制的值,分母部分则是8,也就是 $2^3$, 即 $2^{frac}$

对于非规格化, f = M

对于规格化, f = M-1, 或者说 M = f+1

好,到目前为止我们可以做到两件事情了,第一件是给定一个浮点数的格式,给我它的二进制表示,我可以将这个浮点数的值计算出来

比如 1 01111 001, 那么很明显首先根据符号位判断是一个负数,指数部分为5位,所以可以计算出Bias = $2^{5-1}-1 = 15$. 指数部分并非全0所以是一个规格化的数, 所以 E = e-Bias = 15-15=0. 再看小数部分的值为 f = 1/8,由于是规格化所以 M = f+1 = 9/8, 所以最后的值为 $2^0 \times \frac{9}{8} = 9/8$ ,加个负号 -9/8

再比如 1 0111 0010, 首先是一个负数, 指数4位 Bias = 7, 规格化, E = 7-7 = 0. 小数部分 f = 2/16, M = f+1 = 18/16,所以值为 -18/16 = -9/8

最后来一个 0 00000 111, 正数, 指数5位 Bias = 15, 非规格化 E = -14, f = 7/8 = M, 所以值为 $\frac{7}{8} \times 2^{-14} = 7/2^{17}$

总结一下做题技巧, 半秒钟扫一眼符号位记在脑子里, 看指数多少位, 算一下 Bias, 一定注意是 2的exp-1次幂 -1 ,exp-1如果记错了那可糟糕了. 然后看一眼指数部分是不是全0, 如果全零那就是非规格化,否则是规格化. 根据规格化还是非规格化计算 E, 算一下f然后判断是否加1, 乘起来最后把符号位加上,结果化简一下就可以了

这个过程主要是熟能生巧, 课后习题练几道考试绝对不慌.

第二件事情可就头大了,那就是给我一个数,我能不能写出来它的二进制的浮点数格式?

写这个可是相当耗脑筋,而且几乎除了做几道习题其余时间毫无用处,在这之前我们不妨先回答一下第三个问题

这里的分隔线提到的非规格化和规格化是什么意思呢? 又为什么要这么做呢?

对于任意的一个数,我们总是可以调整指数E使得 M 在0-1之间,即第一位是0.xxx的话就小数点右移

小数域frac解释为描述小数值f,其中 $0\leq f < 1$, 而有效数M的定义为 1+f. 既然第一位总是1,那么我们就不需要显示的来表示它了

为什么会有偏置值Bias呢? 首先我们考虑到一个小数肯定是既可以表示较大的数,也可以表示较小的数(指趋近于0),那么这时候指数就一定是负数才可以.

负数的表示方法再补码的时候是使用最高位的1来表示的,经过简单的对比计算不难发现.如果浮点数的格式中留给exp的位数有4位. 那么原先补码的方式区分正负的话可以表示的范围为 -8 ~ 7, 如果以上文提到的计算方式则是 -6 ~ 7, 范围反而更小了?

这里的范围是 -6~7是因为最小值是1-7=-6, 而最大值由于规格化的情况下指数部分不能全为1,全为1是一种特殊情况表示无穷,所以最大值为1110(14),14-7=7
补码的形式这个取值范围暂时没有考虑需要去除无穷的情况,我们也可以假定 1000(即-8)是代表无穷

但是规格化非规格化区分的时候采用了f/f+1来计算有效数 M, 即如果是非规格化就是 1-Bias作为指数,f作为M; 如果是规格化则是 e-Bias作为指数, f+1作为 M. 采用1-Bias的一个好处是 使得最大非规格化数到最小规格化数的变化非常平滑

另外可以观察到这个表达式具有一个很有趣的属性, 如果我们忽略符号位(s),将后面的(exp)和(frac)解释为无符号整数,他们就是按照升序排列的,就像它们表示的浮点数一样.这并不是偶然的,IEEE格式如此设计就是为了 浮点数能够使用整数排序函数进行排序.

而如果是补码的形式,即造成了混乱了排序,需要额外处理指数部分的正负,还有过渡不平滑等等问题.

特殊情况

特殊情况有两种,一种是指数部分(exp)全为1,并且(frac)全为0,这时候表示的是无穷,根据符号位判断是正无穷或者负无穷

另一种情况是(exp)全1,但是(frac)不全1,这种情况代表NaN(Not a Number),用于处理异常情况,无效运算,数学上未定义的情况. 例如:负数的平方根

舍入

上图可以看出浮点数的范围和精度有限,对于该规格的8位最小是0,其次就是1/512了,240以上的数也无法表示. 即使是对于精度更高的float/double 也同样存在无法表示的数据

这时候我们想有一种系统的方法,能够找到最接近的匹配值,它可以用期望的浮点形式表示出来

参考IEEE 754 的舍入规则

常用的舍入方式分为四种,分别是向零舍入,向上舍入,向下舍入,向偶数舍入

其中向零舍入,向上舍入,向下舍入就不再赘述了,大家看一下上图结合实际很清晰明了,这里着重讲一下向偶数舍入

计算机中为什么要采用向偶数舍入的方式呢?

前文已经提及了计算机可能无法精确表示某一个浮点数,所以在计算的过程中舍入的情况必须要考虑.

如果我们只采用向上或者向下中的一种，就会造成平均数过大或者过小，实际上这时候就是引入了统计偏差。如果是采用偶数舍入，则有一半的机会是向上舍入，一半的机会是向下舍入，这样子可以在一定程度上避免统计偏差

如何使用向偶数舍入计算呢?

这里首先要提到一个很重要的概念, 中间值. 中间值的确定首先要看我们要保留多少位有效数字,或者说我们要精确到哪一位.

以十进制为例,比如对于 1.2349999 舍入到小数点后两位,也就是百分位.那么中间值就是舍入位下一位为该进制的中间值,后面全为0; 对于这个题目来说,中间值就是小数点后第三位为5,其后全为0,即 1.2350000

当具体的值大于中间值的时候，向上舍入

当具体的值小于中间值的时候，向下舍入

当具体的值等于中间值的时候，向偶数舍入

所以本题舍入的情况是实际值 1.2349999 小于中间值 1.2350000, 故向下舍入为 1.23. 如果是 1.2350001 则大于中间值舍入为 1.24

那么如果刚好是 1.2350000 如何进行偶数舍入呢? 这时就看舍入位是奇数还是偶数. 此时舍入位为3是偶数,所以向偶数4舍入得到 1.24. 如果是 1.2450000 则舍入位4为偶数所以还是向偶数4舍入得到1.24

接下来以二进制为例，有效位数保留到小数点后两位

这里值得一提的是二进制中间值为什么是1呢? 如果是三进制的话012我们肯定很容易的得到1是中间值.但是二进制实际上只有两个值0/1为什么就选择了1而不是0呢?

实际上这个问题也很好解释,因为舍入位下一位选择中间值,而其之后全为0,所以对于二进制来说的它情况如下

00 : 一定会向下舍入

01 : 一定会向下舍入

10 : 不确定,刚好等于中间值了所以向偶数舍入

11 : 一定会向上舍入

接近一个3:2的舍入情况,而如果选择0作为中间值可以看出来除了00是偶数舍入,01,10,11都是向上舍入了就变成了1:4的分类了,显然1作为二进制的中间值是合理的.这也就同时解释了偶数进制(十进制,十六进制)为什么采用一半(5,8)作为中间值了.

写到此处关于浮点数的基本知识点说的差不多了,接下来我们来一些习题的实战吧.

我们先来解决到之前遗留下来的那个问题,给我一个值,我如何写出它的二进制的浮点数格式?

根据这张图我们可以明显的看出一个非规格化和规格化的分界线,即7/512和8/512

前文提到过IEEE754标准的浮点数是一个升序的,所以第一步是计算出非规格化的最大值并且判断这个数是规格化还是非规格化,如果需要转化的数值比它小,那么就一定是非规格化表示,否则使用规格化表示

第一步判断之后就可以进入第二步了,首先如果是非规格化,那么很显然(exp)的部分全是0,符号位一眼鉴定,所以实际上只需要计算(frac)的部分就可以了. 我们可以通过(exp)的位数计算出来Bias,这样就得到了E=1-Bias,接下来只需要 $\frac{V}{2^E}$ 就可以计算出有效数 M ,然后再根据(frac)的位数算出分母是多少,然后就可以计算出分子,转换成二进制就可以了

如果判断是规格化,那就有点费劲了. 因为我们需要同时考虑(exp)的部分和(frac)的部分. 这时候需要先观察一下给的值是多少,因为最后算出的有效数M一定是1-2之间的,然后这个M再乘上指数2^E得到的结果,所以我们可以通过结果反推指数的值, 比如结果是35,那么很可能这个指数就是5,因为 $2^5=32$ ,再乘上一个1.多的小数就有可能得到35,大概意思如此.

简单判断出来指数的E的值之后就可以通过规格化的公式反向推出e=E+Bias了,这就是(exp)的部分了,M是通过 $\frac{V}{2^E}$ 计算出来, f = M-1 然后再转换成二进制,最后得到(frac)部分

这一部分实在是麻烦,考试或者做题的时候需要保持头脑清醒,计算准确,需要勤加练习

易错易忘的地方有几个,规格化和非规格化中1-Bias还是e-Bias,要不要f+1,Bias的计算方法,化简的时候注意是2的幂.

有的时候还会遇到一些棘手的情况比如没办法表示,只能依靠舍入来计算一个近似的结果,或者发现规格化的最大值也无法表示这个数值,只能选择无穷了.

这里直接引用了CSAPP书中的一道习题,这里中文版和英文版的题目内容不同,本文采用英文版的习题

A格式是1(s)+5(exp)+3(frac), B格式是1(s)+4(exp)+4(frac). 题目要求将A的值转换为最接近的B的值,如果需要舍入采用向正无穷舍入

A-Bits	A-Value	B-Bits	B-value
1 01111 001	-9/8	1 0111 0010	-9/8
0 10110 011
1 00111 010
0 00000 111
1 11100 000
0 10111 100

题目答案如下:

A-Bits	A-Value	B-Bits	B-value
1 01111 001	-9/8	1 0111 0010	-9/8
0 10110 011	176	0 1110 0110	176
1 00111 010	-5/1024	1 0000 0101	-5/1024
0 00000 111	$7/2^{17}$	0 0000 0001	$2^{-10}$
1 11100 000	-8192	1 1110 1111	-248
0 10111 100	384	0 1111 0000	$+\infin$

最后是datalab中最后的三道浮点数和整数之间的题目

//float
/*
 * floatScale2 - Return bit-level equivalent of expression 2*f for
 *   floating point argument f.
 *   Both the argument and result are passed as unsigned int's, but
 *   they are to be interpreted as the bit-level representation of
 *   single-precision floating point values.
 *   When argument is NaN, return argument
 *   Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
 *   Max ops: 30
 *   Rating: 4
 */
unsigned floatScale2(unsigned uf) {
    int exp_mask = 0x7f800000;
    int exp = (uf&exp_mask)>>23;
    int frac_mask = 0x7fffff;
    int frac = uf & frac_mask;
    if (exp == 0) {
        if (frac>>23&1) {
            frac = frac * 2 - 0x7fffff;
        } else {
            frac = frac << 1;
        }
        return (uf & ~frac_mask) | frac;
    } else if (exp == 255) {
        return uf;
    } else {
        return (uf & ~exp_mask) | (exp+1)<<23;
    }
}
/*
 * floatFloat2Int - Return bit-level equivalent of expression (int) f
 *   for floating point argument f.
 *   Argument is passed as unsigned int, but
 *   it is to be interpreted as the bit-level representation of a
 *   single-precision floating point value.
 *   Anything out of range (including NaN and infinity) should return
 *   0x80000000u.
 *   Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
 *   Max ops: 30
 *   Rating: 4
 */
int floatFloat2Int(unsigned uf) {
    int exp_mask = 0x7f800000;
    int frac_mask = 0x7fffff;
    int exp = (uf & exp_mask)>>23;
    int frac = uf & frac_mask;
    int signal = uf>>31&1;
    int bias;
    int ans;
    if (exp < 127) {
        return 0;
    } else if (exp == 255 || exp > 127+31) {
        return 0x80000000;
    } else {
        if (exp==127+31){
            if (frac==0 && signal == 1) {
                return 0x80000000;
            } else {
                return 0x80000000;
            }
        } else {
            bias = exp-127;
            if (bias >= 23) {
                ans = (1<<bias) + (1<<bias>>23)*frac;
            } else {
                ans = 1<<bias;
            }
            return signal ? -ans:ans;
        }
    }
}
/*
 * floatPower2 - Return bit-level equivalent of the expression 2.0^x
 *   (2.0 raised to the power x) for any 32-bit integer x.
 *
 *   The unsigned value that is returned should have the identical bit
 *   representation as the single-precision floating-point number 2.0^x.
 *   If the result is too small to be represented as a denorm, return
 *   0. If too large, return +INF.
 *
 *   Legal ops: Any integer/unsigned operations incl. ||, &&. Also if, while
 *   Max ops: 30
 *   Rating: 4
 */
unsigned floatPower2(int x) {
    int frac, exp;
    if (x < -149) return 0;
    else if (x >= -149 && x <= -127) {
        frac = x+149;
        return 1 << frac;
    } else if (x<128) {
        exp = x+127;
        return exp << 23;
    } else {
        return 255 << 23;
    }
}