title: GAN网络详解(三) - WGAN-CP 与 WGAN-GP date: 2022-05-18 23:08:13 tags: GAN
本文将会介绍WGAN-CP和它的改进版本WGAN-GP
WGAN-CP
参考文章GAN到WGAN,作者连续五篇文章非常详尽的分析了WGAN,读完之后受益匪浅
鉴于GAN网络存在的种种问题,那么我们应该寻求一个新的距离来替代JS.该文认为需要对“生成分布与真实分布之间的距离”探索一种更合适的度量方法。作者们把眼光转向了Earth-Mover距离,简称EM距离,又称Wasserstein距离
{% note info %} W距离是最优传输(Optimal Transportation)理论中的关键概念,而最优传输及W距离的场景可以用一个非常的简单实际问题来描述:有一座土山,需要把它搬运到另外一个地方堆积成一座新的土山,要求整个过程中土的总质量不能改变。最优传输问题即在诸多的运土方案中,寻找代价最小的那个方案,而W距离指的就是这个最小代价
W距离也拥有一个非常形象的“花名”——“推土机距离”(Earth Mover's Distance) {% endnote %}
那么什么是最优传输的传输计划和传输代价呢?
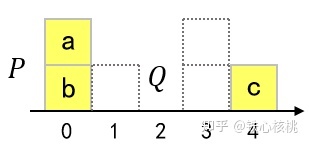
下面以一个简单的挪箱子问题作为示例,黄色箱堆为P,需要将其挪动为虚线框所示的样子。我们这样定义代价:挪动每个箱子的代价为该箱子的质量与位移的乘积,那么传输代价为挪动所有箱子代价的总和.
假设每个箱子质量相同,现在我们想让P状态下所有的黄色箱子挪到虚线中(状态Q),最小的传输代价是多少呢?
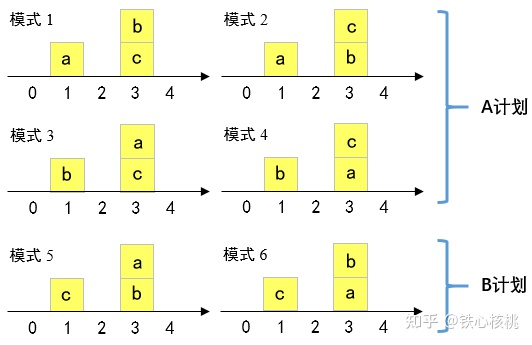
最终的Q状态有三个位置,也就是说最终有3!种移动方法,由于所有箱子质量相同,故可以分为两种计划
{% note info %} 这里我们以下标01234来代指计划移动的方式
- A计划就是将一个0位置的方块移动到1位置,然后将0,4两个位置的方块移动到3
- B计划就是将两个0位置的方块移动到3位置,然后将4位置的一个方块移动到1
对于A计划传输代价为 1+3+1 = 5
对于B计划传输代价为 3x2+3 = 9
这样我们就完成了从P到Q的状态转移,完成了一次传输.
显而易见,A传输计划的传输代价最小,故上述例子的W距离为5 {% endnote %}
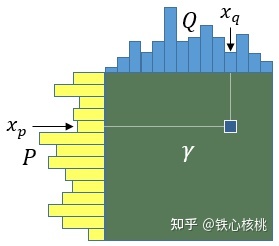
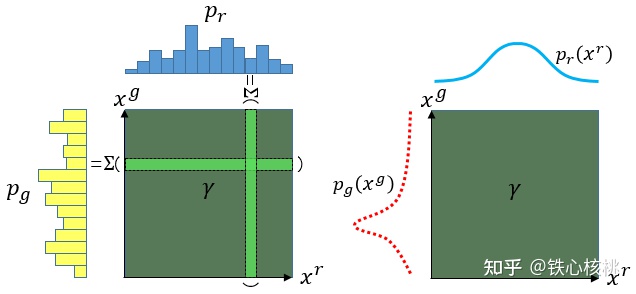
传输计划可以很方便的用矩阵形式表示,即“传输矩阵”。给定一个“运输计划”,即可确定一个矩阵$\gamma$,其元素$\gamma(x_p,x_q)$,表示从P中$x_p$位置“运输”到Q中$x_q$位置的“土量”
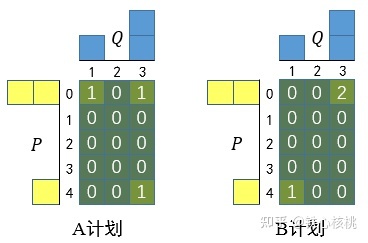
以上面挪箱子的问题为例,其中A、B计划对应的传输矩阵分别为
{% note info %} 其中对应位置的数字表示移动了几个方块,代价计算的方式就是x y的差值乘数字
对于A, $cost_A = |0-1|\times 1 + |0-3|\times 1+|4-3|\times 1 = 5$
对于B, $cost_B = |0-3|\times 2 + |4-1|\times 1 = 9$ {% endnote %}
所以可以得到总传输矩阵为
$$ B(\gamma) = \sum\limits_{x_p,x_q}\gamma(x_p,x_q)||x_p -x_q|| $$
所以我们要求得的最小代价也就是 $W(P,Q) = \min\limits_{\gamma\in\prod} B(\gamma)$
所以可以很容易看出,只要获得最优传输矩阵,对应的W距离就可以很容易的计算得到
所以对于两个分布P,Q,他的传输矩阵其实表达了一个联合分布
艰难的回忆起概率论的知识...
$p_g,p_r$对应的边缘分布为
$$ p_g(x^g) = \int_{x^r}\gamma(x^g,x^r)dx^r\ p_r(x^r) = \int_{x^g}\gamma(x^g,x^r)dx^g $$
所以我们转换一下上述的$B(\gamma)$,可以得到
$$ W(p_g,p_r) = \inf_{\gamma\in\prod}\iint_{x^g,x^r}\gamma(x^g,x^r)||x^g,x^r||dx^gdx^r $$
其中$\gamma(x^g,x^r)$是一个联合分布,$||x^g,x^r||$为随机变量的函数,这个公式又可以用数学期望来化简,于是我们用一个非常简洁的期望表达式来表示W距离
$$ W(p_g,p_r) = \inf_{\gamma\in\prod}E_{(x^g,x^r)\thicksim\gamma}||x^g,x^r|| $$
这便是最终的Wasserstein距离的表达式由来,这种方式要比直接看定义要好理解的很多.
从上面的推导我们可以很容易的看出,以W距离作为分布之间相似性度量很不错,概括起来有以下三条优点:
- 交换性:$W(p_g,p_r) = W(p_r,p_g)$这一点比KL散度强多了
- 非负性:$W(p_g,p_r)>0$,当$p_g=p_r$时,$W(p_g,p_r)=0$,原地不动自然不用耗费体力
- 指标性:当$Dist(p_g,p_r)>Dist(p_{g'},p_{r'})$时,$W(p_g,p_r)>W(p_{g'},p_{r'})$,这正是散度的“软肋”啊.距离与代价正相关很有利于训练,计算梯度
Wasserstein距离相比KL散度、JS散度的优越性在于,即便两个分布没有重叠,Wasserstein距离仍然能够反映它们的远近
{% note success %} KL散度和JS散度是突变的,要么最大要么最小,Wasserstein距离却是平滑的,如果我们要用梯度下降法优化$\theta$这个参数,前两者根本提供不了梯度,Wasserstein距离却可以。类似地,在高维空间中如果两个分布不重叠或者重叠部分可忽略,则KL和JS既反映不了远近,也提供不了梯度,但是Wasserstein却可以提供有意义的梯度。 {% endnote %}
看起来Wasserstein距离是一个挺不错的距离啊!但是它的缺点也是直观的,这就是太难算!直观上看我们要将所有可能的联合分布试一遍才能找到那个使得代价最小的分布.况且WGAN其实也并不是要求这个距离是多少,首先是基于线性规划的W距离在针对多状态高维数据的计算几乎不可能实现,100维,1000维,这种计算量实在是太可怕了.
{% note info %} 如果想要了解如何快速计算两个分布的W距离,我们可以使用线性规划(Linear Programming)的方式先求解最优传输矩阵,最优传输矩阵一旦获得,W距离的计算也就易如反掌。
参考https://zhuanlan.zhihu.com/p/358330515 {% endnote %}
求距离不是我们的目的,我们真正想要的是使得W距离取得最小的那个$p_g$,我们不是求最小值,我们是求下确界
求下确界而不是最小值是因为最小值并不一定存在,例如某些渐进的函数 $e^x$诸如此类
所以现在的问题是我们要求的不是W,而是他的约束条件$p_g$,这怎么求?
{% note info %} 这一部分的数学推导十分复杂,作者也用了很严密的数学证明,其中涉及的公式证明较多,主要利用了对偶线性规划求解W距离,1-利普希茨连续条件(1-L)等方法. 笔者自知数学功底较差,也并不指望能够给读者完整的解释清楚 有兴趣的话可以去阅读一下原论文附录中的证明过程,或者浏览对偶线性规划与W-GAN,十分详尽 {% endnote %}
简而言之,我们得到了最终的结论
$$ W(p_g,p_r) = \sup\limits_{f\in 1-Lipschitz}E_{x\thicksim p_r(x)}[f(x)]-E_{x\thicksim p_g(x)}[f(x)] $$
{% note info %} 其中 1-Lipschits 是1-利普希茨连续条件(Lipschitz continuity)
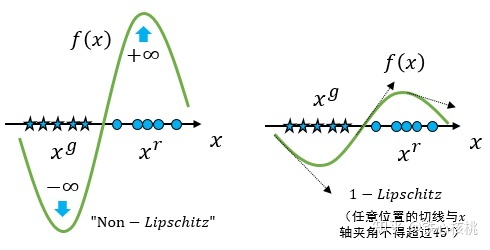
K-普希茨连续条件的定义是,对于任意的$x_i,x_h\in R^n$,都存在常数K使得$|f(x_i)-f(x_j)|\le 1K||x_i-x_j||$
直白一点说就是约束了这个函数f(x)的梯度,不能超过K这个值.
1-L就是所有点的梯度不能超过1 {% endnote %}
上式中f满足1−利普希茨条件。若其满足K−利普希茨条件,则得到的距离为$K\cdot W(p_g,p_r)$
假设有一族满足K-利普希茨条件的参数化函数$f_w$,我们可以得到一个近似的表示
$$ K\cdot W(p_g,p_r) \approx \sup\limits_{f\in 1--Lipschitz}E_{x\thicksim p_r(x)}[f_w(x)]-E_{x\thicksim p_g(x)}[f_w(x)] $$
W-GAN即将上式中的$f_w(x)$构造为一个参数为$w$神经网络结构,由于神经网络的拟合能力足够强大,我们有理由相信,这样定义出来的一系列$f_w(x)$虽然无法囊括所有可能,但是也足以高度近似公式要求的限制 $f\in 1-Lipschitz$
这里的 f 应该满足以下两个条件
- 第一,$f_w(x)$需要表达距离,而不是概率,所以不能像标准GAN中判别器那样输出概率了。不过这好办,只要在在网络最后的位置不使用Sigmoid激活函数即可
- 第二,$f_w(x)$要满足K-利普希茨条件.我们要的并非距离本身,我们后续是要最小化这个距离,因此到K取多少都无所谓,只要要求$f_w(x)$不要“跑飞”即可.因此在W-GAN中,使用了一种简单的权重裁剪(weight clipping)策略
即将$f_w(x)$中的参数$w$限定在一个给定的范围 $[-c,c]$ 之内.权重裁剪的出发点很简单:输入数据固定,函数输出值只与参数有关,而参数范围固定,则随着输入的变化,输出的改变也会限定在一个有限的范围内
此时关于输入样本 $x$ 的导数 $\frac{\partial f_w}{\partial x}$也不会超过某个范围,所以一定存在某个不知道的常数 $K$ 使得 $f_w(x)$ 的局部变动幅度不会超过它,Lipschitz连续条件得以满足
总结一下,到此为止,我们可以构造一个含参数 $w$ 、最后一层不是非线性激活层的判别器网络 $f_w(x)$ ,在限制 $w$ 不超过某个范围的条件下,使得 $$ L = E_{x\thicksim p_r(x)}[f_w(x)]-E_{x\thicksim p_g(x)}[f_w(x)] $$
尽可能取最大值,此时 $L$ 就会近似真实分布与生成分布之间的Wasserstein距离
接下来生成器要近似地最小化Wasserstein距离,可以最小化 $L$ ,由于Wasserstein距离的优良性质,我们不需要担心生成器梯度消失的问题
$$ G^* = \argmin\limits_{G}\max\limits_{f_w\in 1-Lipschitz}E_{x\thicksim p_r(x)}[f_w(x)]-E_{z\thicksim p(z)}[f_w(G(z))] $$
{% note info %} 注意这里的极大值极小值可能并不是很好理解,我举一个相似的例子
比如说现在对于函数 $y = e^x+b,b\in [-1,1]$, 我们期望求这个函数在取最大值的时候取得的最小值
很明显应该 b取1, 整个式子变成 $y = e^x+1$ 这时候相较于其他 b的情况是最大的,在这种情况下的最小值(准确说是下确界)是 1
{% endnote %}
再考虑到 $L$ 的第一项与生成器无关,就得到了WGAN的两个loss。
- $G_{loss} = -E_{z\thicksim p(z)}[f_w(G(z))]$
- $D_{loss} = E_{x\thicksim p_r(x)}[f_w(x)]-E_{z\thicksim p(z)}[f_w(G(z))]$
论文中也据此给出了算法的伪代码
{% note info %} 与GAN相比WGAN只改动了四点
- 判别器最后一层去掉sigmoid
- 生成器和判别器的loss不取log
- 每次更新判别器的参数之后把它们的绝对值截断到不超过一个固定常数c
- 不要用基于动量的优化算法(包括momentum和Adam),推荐RMSProp
前三点都是从理论分析中得到的,已经介绍完毕;第四点却是作者从实验中发现的,属于trick,相对比较“玄”。作者发现如果使用Adam,判别器的loss有时候会崩掉,当它崩掉时,Adam给出的更新方向与梯度方向夹角的cos值就变成负数,更新方向与梯度方向南辕北辙,这意味着判别器的loss梯度是不稳定的,所以不适合用Adam这类基于动量的优化算法。作者改用RMSProp之后,问题就解决了,因为RMSProp适合梯度不稳定的情况
具体的WGAN-CP的代码实现可以参考这里 {% endnote %}
总结:
WGAN前作分析了Ian Goodfellow提出的原始GAN两种形式各自的问题
- 第一种形式等价在最优判别器下等价于最小化生成分布与真实分布之间的JS散度,由于随机生成分布很难与真实分布有不可忽略的重叠以及JS散度的突变特性,使得生成器面临梯度消失的问题
- 第二种形式(-logD)在最优判别器下等价于既要最小化生成分布与真实分布直接的KL散度,又要最大化其JS散度,相互矛盾,导致梯度不稳定,而且KL散度的不对称性使得生成器宁可丧失多样性也不愿丧失准确性,导致collapse mode现象。
WGAN本作引入了Wasserstein距离,由于它相对KL散度与JS散度具有优越的平滑特性,理论上可以解决梯度消失问题。接着通过数学变换将Wasserstein距离写成可求解的形式,利用一个参数数值范围受限的判别器神经网络来最大化这个形式,就可以近似Wasserstein距离。在此近似最优判别器下优化生成器使得Wasserstein距离缩小,就能有效拉近生成分布与真实分布。WGAN既解决了训练不稳定的问题,也提供了一个可靠的训练进程指标,而且该指标确实与生成样本的质量高度相关
WGAN-GP
前文提到了我们最后利用 1-L约束可以得到的最终优化方程
$$ G^* = \argmin\limits_{G}\max\limits_{f_w\in 1-Lipschitz}E_{x\thicksim p_r(x)}[f_w(x)]-E_{z\thicksim p(z)}[f_w(G(z))] $$
实际我们也说了,是不是1都无所谓,只要函数别“跑飞”了就行。理论上很圆满,但是W-GAN在实现时却选择了一个略显粗糙的方法——权重裁剪 weight clipping,按照预先设定的截断范围,通过人为硬性的权重截断方式,以限制函数参数的方式来限制取值范围,这种想法显然是极其朴素的
从效果角度看,权重裁剪也是存在大问题的。正是因为这个原因,才有了本篇文章介绍具有梯度惩罚(Gradient Penalty, GP)策略的W-GAN,即W-GAN-GP
- 权重裁剪有什么问题么?
{% note info %}
- 问题1: 参数二值化
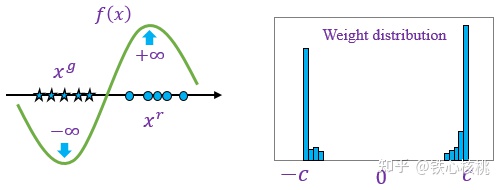
W-GAN的优化目标是两个数学期望的差,两个期望之差自然表示真假两路数据被 $f_w$ 作用后平均值之间的差值,简单说就是函数要在两类数据上“扯开”
试想我们在权重裁剪中给定常数 $c$, 比如 $c=0.01$ 后,要求上面的差值越大越好,且要求参数不能小于-c且不能大于c,这样的操作势必导致参数的向着-c和c聚集,形成两极分化, $f_w$ 即退化为一个二值神经网络,表现能力将异常低下
判别器会非常倾向于学习一个简单的映射函数,都已经可以直接视为一个二值神经网络了,判别器没能充分利用自身的模型能力,经过它回传给生成器的梯度也会跟着变差。
- 问题2: 训练难调节
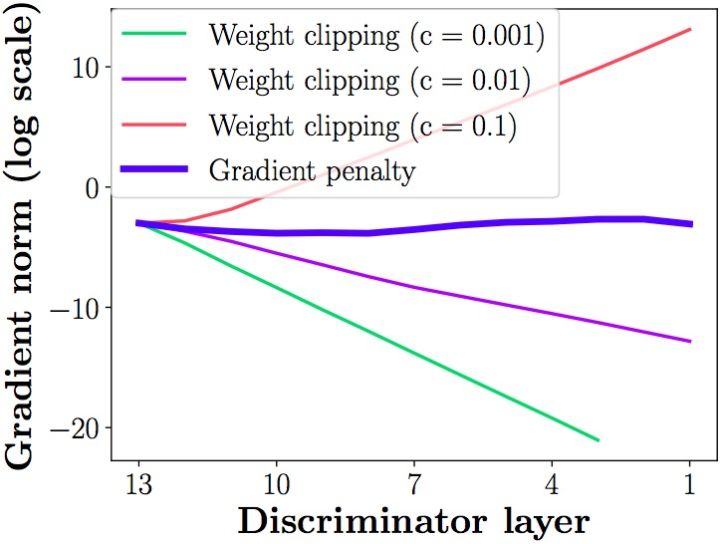
权重截断直接在参数上“做手术”,硬性将权重设定在 $[-c,c]$ 范围,这存在将本来大的参数截小和将本来小的参数截大的可能。因此截断值的设定至关重要,否则要么梯度消失(梯度为0),要么梯度爆炸(梯度为无穷大)
原因是判别器是一个多层网络,如果我们把clipping threshold设得稍微小了一点,每经过一层网络,梯度就变小一点点,多层之后就会指数衰减;反之,如果设得稍微大了一点,每经过一层网络,梯度变大一点点,多层之后就会指数爆炸。只有设得不大不小,才能让生成器获得恰到好处的回传梯度,然而在实际应用中这个平衡区域可能很狭窄,就会给调参工作带来麻烦
需要选取一个合适的权重裁剪的值才可以使这个网络训练梯度稳定
{% endnote %}
- 所以如何解决权重裁剪的问题呢?
面对上面权重裁剪存在的问题,W-GAN-GP的解决方案为在目标函数上添加一个梯度惩罚项(Gradient Penalty, GP),“罚出”一个利普希茨条件
作者给出了两个版本的惩罚梯度
- 版本1
$$ \omega^* = \argmin\limits_{\omega}E_{x\thicksim p_r(x)}[f_w(x)]-E_{z\thicksim p(z)}[f_w(G(z))] + \lambda\max(|\nabla_x f_w(x)|,1) $$
其中 $\lambda$ 为梯度惩罚项的常系数。上面式子可以看出两件事
- 当 $|\nabla_x f_w(x)| \le1$,惩罚项就剩下一个常数$\lambda$
- 当 $|\nabla_x f_w(x)| > 1$,惩罚项为 $\lambda|\nabla_x f_w(x)|$, 这就意味着在求 $\argmin$ 的时候梯度越大则惩罚越大
{% note info %} 意味着梯度超过1就做惩罚,即将梯度尽可能的限制在1之内,尽管版本1更符合1−利普希茨条件的要求,但是其惩罚项中的 $\max$ 不可微,所以并没有选择这个版本 {% endnote %}
- 版本2
$$ \omega^* = \argmin\limits_{\omega}E_{x\thicksim p_r(x)}[f_w(x)]-E_{z\thicksim p(z)}[f_w(G(z))] + \lambda(|\nabla_x f_w(x)|-1)^2 $$
版本2的梯度惩罚项来的更直接,距离1越远则惩罚越大,即将梯度尽可能的等于1。
对于上面两个版本的梯度惩罚,W-GAN中的利普希茨条件只是要求函数 $f_w$ 的梯度有界,但是具体是多少其实无所谓
- 那么具体如何实现呢?
利普希茨连续条件可是要求函数在任意位置的梯度长度不能超过一个定值 $K$,即要求处处成立,上面惩罚项中抽象的 $x$ 就表示任意的位置。但是,所谓的“任意”是无法操作的,所以还是需要带入具体的点
我们期望:
- 选择最好是样本空间的所有点,这样才最“任意”。但是很遗憾,这要求无穷多点,但只有有限的样本点,根本做不到
- 来自于全部的真实数据 $p_{data}$ 和生成数据 $p_g$ ,这样才比较“任意”。但是也很遗憾,一次训练不可能一次性读入全部 $p_{data}$ ,并生成同样多的 $p_g$,还是做不到
{% note success %} W-GAN-GP的解决方案是一个折中方案,选取一个训练小批次中全部的 $x_{data},x_g$,计算它们的随机混合部分
$$ x = \epsilon x_{data} + (1-\epsilon)x_g,\epsilon\thicksim\mathcal{U(0,1)} $$
这样的随机混合近似可以看作是任意点 {% endnote %}
关于梯度惩罚的pytorch实现
def calculate_gradient_penalty(self, real_images, fake_images):
eta = torch.FloatTensor(self.batch_size,1,1,1).uniform_(0,1)
eta = eta.expand(self.batch_size, real_images.size(1), real_images.size(2), real_images.size(3)).to(self.device)
interpolated = eta * real_images + ((1 - eta) * fake_images)
interpolated = interpolated.to(self.device)
# define it to calculate gradient
interpolated = Variable(interpolated, requires_grad=True)
# calculate probability of interpolated examples
prob_interpolated = self.D(interpolated)
# calculate gradients of probabilities with respect to examples
gradients = torch.autograd.grad(outputs=prob_interpolated, inputs=interpolated,
grad_outputs=torch.ones(
prob_interpolated.size()).to(self.device),
create_graph=True, retain_graph=True)[0]
grad_penalty = ((gradients.norm(2, dim=1) - 1) ** 2).mean() * self.lambda_term
return grad_penalty{% note warning %} 论文还讲了一些使用gradient penalty时需要注意的配套事项:由于我们是对每个样本独立地施加梯度惩罚,所以判别器的模型架构中不能使用Batch Normalization,因为它会引入同个batch中不同样本的相互依赖关系。如果需要的话,可以选择其他normalization方法,如Layer Normalization、Weight Normalization和Instance Normalization,这些方法就不会引入样本之间的依赖。论文推荐的是Layer Normalization {% endnote %}
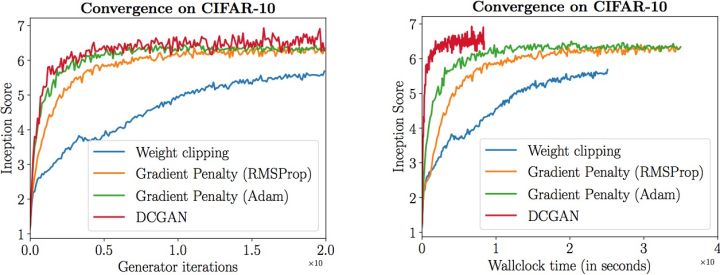
实验表明,gradient penalty能够显著提高训练速度,解决了原始WGAN收敛缓慢的问题
总结与扩展思考
WGAN并不是最GAN网络中最优秀的,随着如今的发展,每年都会有很多GAN相关的论文和模型结构的提出,但是WGAN无疑是一次巨大的飞跃
初次学习了解GAN网络,不仅感叹前人的智慧,非常感谢网络上大佬无私分享的科普文章,阅读之后受益匪浅
笔者个人水平不足,绝大部分内容都为摘抄整理,加入自己的一些理解之后总结的.在对应的引用开头前都标注了原文章的出处,如有侵权即刻删除
从GAN,到使用深度卷积神经网络的DCGAN,到后来改进优化模型的WGAN,到后来进一步加入惩罚梯度的WGAN-GP,以及styleGAN,LSGAN等等等等,真的是学无止境啊!!
说起来这只是一门专选课的结课大作业,我上不上都可以的,不过老师的结课要求很宽松,自由度很高,正巧我之前只是了解过一点GAN相关的内容,并没有深入的学习过.这次正好利用了这次机会初步了解了GAN的相关内容和数学推导,确实令我折服.
{% note info %} 后来也有很多人讨论了关于WGAN的内容,也提出了一些质疑的声音,可以参考这里,有兴趣的可以去了解一下 {% endnote %}
下一篇文章将会用我自己的一个示例来上手体验一下WGAN-GP的训练效果,使用WGAN-GP生成动漫头像