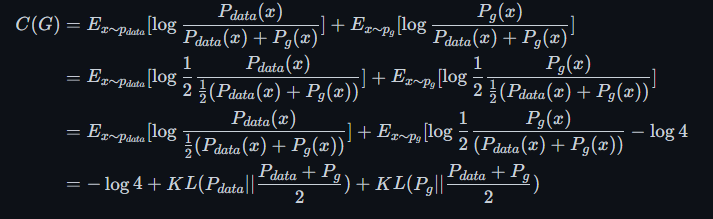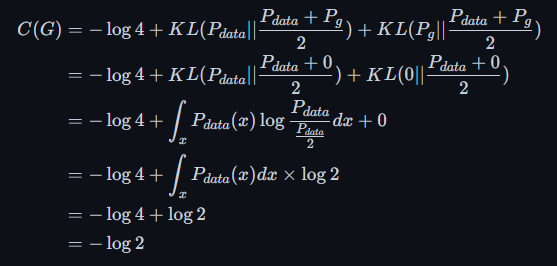title: GAN网络详解(二) - DCGAN以及GAN网络存在的一些问题 date: 2022-05-18 00:12:07 tags: GAN

本文将会介绍DCGAN以及GAN网络存在的一些问题

DCGAN

这篇论文主要针对于GAN网络的经典问题: GANs have been known to be unstable to train, often resulting in generators that produce nonsensical outputs. 进而提出了使用深度卷积神经网络来改进

作者在论文中提出了了一些改进措施,比如

并且作者也指出了一些训练过程中的超参数,权重值,优化器学习率等等,一些细节不再这里赘述了,有兴趣的可以去看一下论文

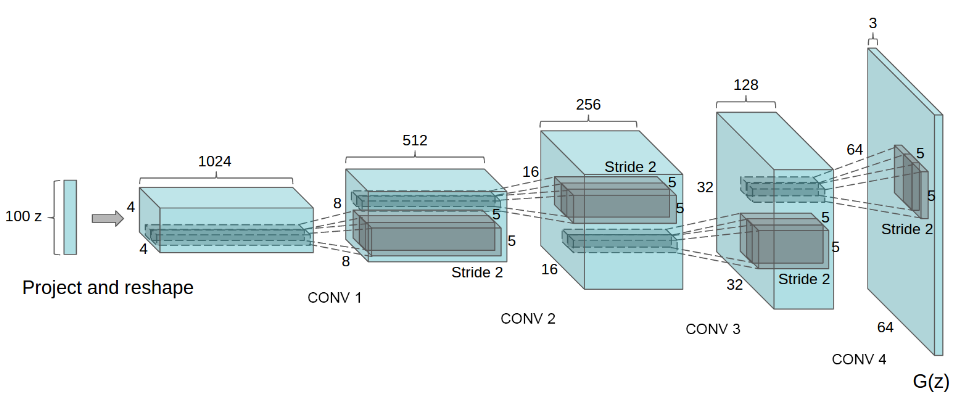
DCGAN的生成器G网络结构如下图所示:

20220518010527

输入是一个100x1x1维的向量,首先将其转置卷积为1024x4x4,然后逐步转置卷积,最后得到一个3x64x64的图片

然后作者也做了跨数据集的分类问题的研究,在Imagenet-1k数据集中训练判别器D然后接一个L2-SVM的分类器,取得了82.8%的准确率.

从结构上来看,DCGAN比常见的判别式网络更加线性,因为连max pooling都没了,不那么线性的部分就只有最后输出图片的Tanh.

潜在空间的探索

作者提到了一个名词 walking the latent space,中译为探索潜在空间

参考文章了解机器学习中的潜在空间

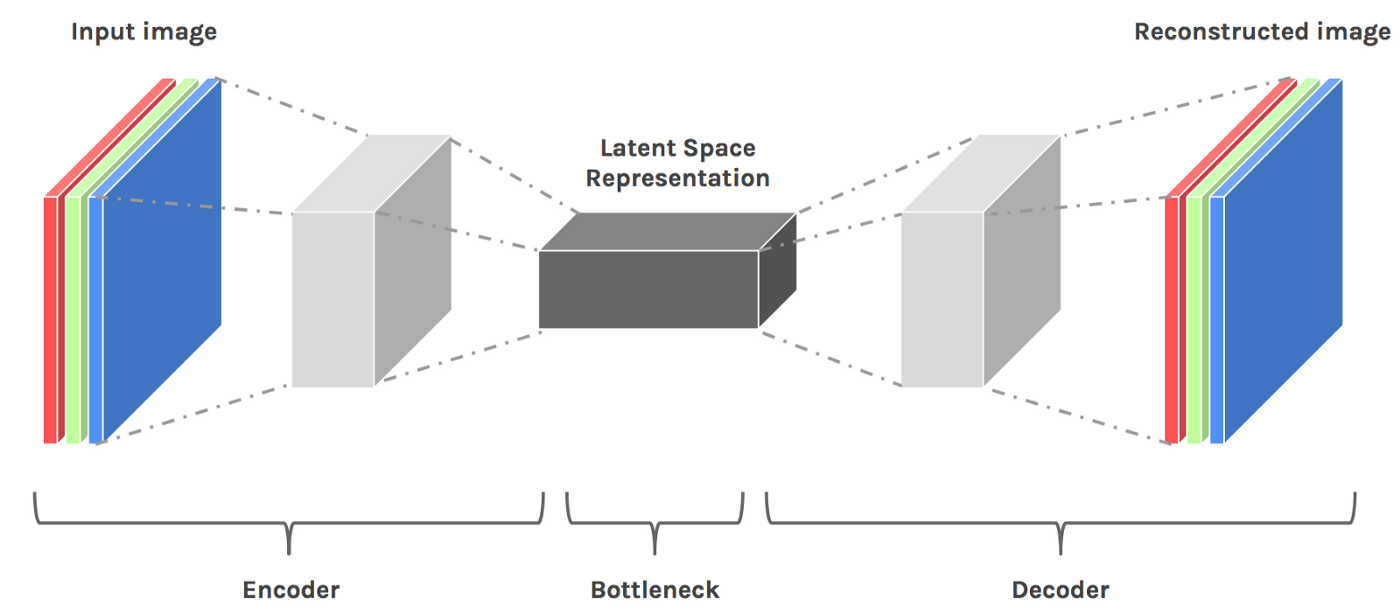
它意味着压缩过的数据.对于经典的手写数据集MNIST,如果我们训练一个神经网络来实现它的分类问题

20220518013126

每次模型通过数据点学习时,图像的维度首先会降低,然后才会最终增加.当维度降低时,我们认为这是一种有损压缩形式.

由于模型需要然后重建压缩数据,因此它必须学会存储所有相关信息并忽略噪声这就是压缩的价值.它使我们能够摆脱任何无关的信息,只关注最重要的功能

这种压缩状态被称为数据的潜在空间.

每当我们绘制点图或想到潜在空间中的点时,我们都可以将它们想象为空间中的坐标,其中相似的点在图上更接近.

一个自然而然的问题是,我们如何想象4D点或n维点甚至非向量的空间,我们是3维生物,无法理解n维空间,我们只能假想一个超空间来映射多维空间的点,而相似的点在这个空间更加"接近"?或者说"相似"?

20220518013758

如果我们看三个图像,两个椅子和一个桌子,我们很容易说两个椅子图像最相似,而桌子与任何一个椅子图像最不同.但是什么让这两把椅子的形象“更相似”呢？椅子具有明显的特征（即靠背,无抽屉,腿之间的连接）。这些都可以被我们的模型通过学习边缘,角度等的模式来“理解”。

如前所述,这些特征被打包在数据的潜在空间表示中。

因此,随着维数的降低,每个图像不同的“无关”信息（即椅子颜色）从我们的潜在空间表示中“删除”,因为只有每个图像最重要的特征存储在潜在空间表示中。

因此,当我们降低维度时,两把椅子的表示变得不那么明显,更加相似。如果我们想象它们在太空中,它们会“更紧密”地结合在一起。

*请注意,这里提到的“接近度”度量是一个模棱两可的术语,而不是明确的欧几里得距离,因为空间中的距离有多种定义。

潜在空间“隐藏”在我们最喜欢的许多图像处理网络、生成模型等中。

虽然潜空间对大多数人来说是隐藏的,但在某些任务中,理解潜空间不仅有帮助,而且是必要的.

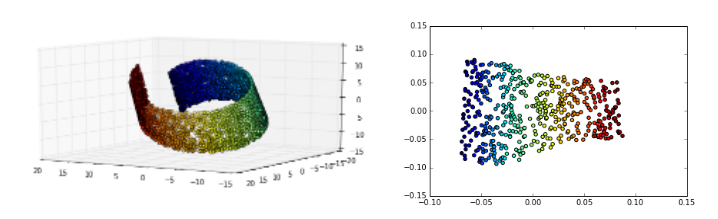
20220518014319

在3D中,我们知道存在类似数据点的组,但是用更高维的数据描绘这些组要困难得多。

通过将数据的维数降低到2D（在这种情况下可以被认为是“潜在空间”表示）,我们能够更轻松地区分数据集中的流形(相似数据组)

我们可以使用在潜在空间中插值的方式来探索不同的面部结构,这也是用来研究GAN网络过程中相当有趣的一个工作

20220518014511

其实很简单,对于两个值X(a1,b1,...z1)和Y(a2,b2,...z2),我们可以使用GAN网络各自生成他们对应的图片,这没有问题.

而线性插值就是依次探索这两个高维点之间的空间,可以用来研究它们之间的过渡/变化过程

import torch
X = torch.randn((5,5,5,5))
Y = torch.randn((5,5,5,5))

alpha = 0
walk_step = 100
images = []
G = generator()

for i in range(walk_step):
    point = alpha * X + (1-alpha) * Y
    images.append(G(point))
    alpha = alpha + 1/walk_step

# then do visiualization for images to see latent space for generator

上图就体现出了这个转变的过程

{% note info %} 关于latent space 的相关内容这里再扩展一些,因为目前做的都是线性插值,即直接取了两点之间的直线,有人认为在高维空间中数据其实分布在帐篷布上,但是线性插值的方法其实走的是帐篷杆,应该用一种更好的方式Slerp.详见知乎-行走在GAN的Latent Space,作者也讨论了Great Circle也做了一些实验,我觉得还是很值得一看的. {% endnote %}

总结来说DCGAN依靠的是对判别器和生成器的架构进行实验枚举,最终找到一组比较好的网络架构设置,但是实际上是治标不治本,没有彻底解决问题.GAN网络的训练依旧十分困难

GAN网络存在的问题

参考文章:

WGAN的来龙去脉

令人拍案叫绝的WGAN

为什么GAN网络难以训练

在介绍WGAN之前,我们需要先了解GAN网络存在的问题,WGAN的一作作者Martin Arjovsky在2017年先后参与了三篇相关论文,第一篇论文"Towards Principled Methods for Training Generative Adversarial Networks",这篇论文是WGAN发表前的铺垫,它最大的贡献是从理论上解释了GAN训练不稳定的原因.

人们在应用GAN时经常发现一个现象：不能把Discriminator训练得太好,否则Generator的性能很难提升上去.该文以此为出发点分析了GAN目标函数的理论缺陷.

在上一节中,我们提到了GAN网络的目标函数

$$ \min\limits_{G}\max\limits_{D}V(D,G) = E_{x\thicksim p_{data(x)}}[\log D(x)] + E_{z\thicksim p_{z(z)}}[\log(1-D(G(z)))] $$

同时证明了,固定Generator时,最优的Discriminator的取值是

$$ D^*_G(x) = \frac{P_{data}(x)}{P_{data}(x) + P_g(x)} $$

所以在面对最优Discriminator时,Generator的优化目标就变成了

20220518000942

写成JS散度的形式就是

$$ C(G) = -\log4 + 2*JSD(p_{data}||p_g) $$

所以现在这个问题被转化为:在最优判别器的下,我们可以把原始GAN定义的生成器loss等价变换为最小化真实分布$P_{data}$与生成分布$P_g$之间的JS散度。我们越训练判别器,它就越接近最优,最小化生成器的loss也就会越近似于最小化$P_{data}和$P_g$之间的JS散度

问题就出在这个JS散度上。我们会希望如果两个分布之间越接近它们的JS散度越小,我们通过优化JS散度就能将$P_g$"拉向"真实分布$P_{data}$

这个希望在两个分布有所重叠的时候是成立的,也就是最终的优化目标$P_g = P_{data}$.但是如果两个分布完全没有重叠的部分,或者它们重叠的部分可忽略,它们的JS散度是多少呢？

{% note info %} GAN中的生成器一般是从某个低维（比如100维）的随机分布中采样出一个编码向量,再经过一个神经网络生成出一个高维样本（比如64x64的图片就有4096维）。当生成器的参数固定时,生成样本的概率分布虽然是定义在4096维的空间上,但它本身所有可能产生的变化已经被那个100维的随机分布限定了,其本质维度就是100,再考虑到神经网络带来的映射降维,最终可能比100还小,所以生成样本分布的支撑集就在4096维空间中构成一个最多100维的低维流形,“撑不满”整个高维空间.

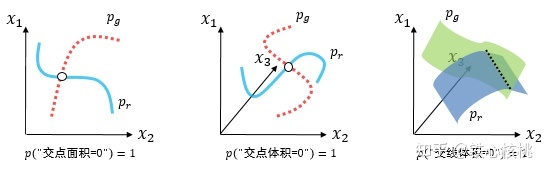
“撑不满”就会导致真实分布与生成分布难以“碰到面”,这很容易在二维空间中理解：

三维空间中也是类似的,随机取两个曲面,它们之间最多就是比较有可能存在交叉线,但是交叉线比曲面低一个维度,面积（测度）是0,可忽略。

v2-45852cfbb4fcf2943e7d6eafcb9ed054_720w

{% endnote %}

那么回到刚才的问题,如何计算两个分布的JS散度呢? 我们惊讶的发现这是一个定值 $\log2$

对于任意的空间中任意选定的一点x,在真实分布$P_{data}$与生成分布$P_g$中的概率有四种情况

换句话说,无论真实分布$P_{data}$与生成分布$P_g$是远在天边,还是近在眼前,只要它们俩没有一点重叠或者重叠部分可忽略,JS散度就固定是常数,而这对于梯度下降方法意味着梯度为0！此时对于最优判别器来说,生成器肯定是得不到一丁点梯度信息的；即使对于接近最优的判别器来说,生成器也有很大机会面临梯度消失的问题

参考难以优化的GAN

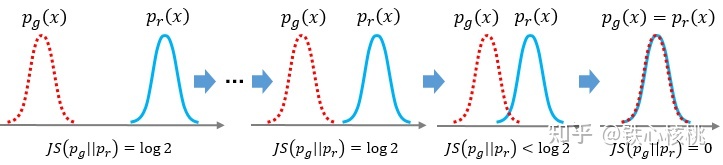
https://zhuanlan.zhihu.com/p/357141352

我们就得到了WGAN前作中关于生成器梯度消失的第一个论证：在（近似）最优判别器下,最小化生成器的loss等价于最小化$P_{data}$与$P_g$之间的JS散度,而由于$P_{data}$与$P_g$几乎不可能有不可忽略的重叠,所以无论它们相距多远JS散度都是常数$-\log2$,最终导致生成器的梯度（近似）为0,梯度消失

JS散度是f散度的一种,所有的f散度都具有一个问题,那就是在两个分布几乎没有交集的时候,散度为一个常数,这意味着梯度为零,而我们是使用梯度下降求解的,所以这意味着我们无法很好地完成优化

该文花了大量的篇幅进行数学推导,证明在一般的情况下,上述有关JS散度的目标函数会带来梯度消失的问题。也就是说,如果Discriminator训练得太好,Generator就无法得到足够的梯度继续优化,而如果Discriminator训练得太弱,指示作用不显著,同样不能让Generator进行有效的学习。这样一来,Discriminator的训练火候就非常难把控,这就是GAN训练难的根源.

mode dropping / mode collapse

{% note info %} 指的是生成样本只集中于部分的mode从而缺乏多样性的情况。例如,MNIST数据分布一共有10个mode（0到9共10个数字）,如果Generator生成的样本几乎只有其中某个数字,那么就是出现了很严重的mode collapse现象

即生成器仅仅生成部分重复的图片,缺乏多样性 {% endnote %}

mode collapse在GAN的训练中也非常的常见,比如将会在下一节中出现的示例,我自己的在使用DCGAN训练一个生成动漫头像的GAN网络,出现了十分明显的 mode collapse的现象

epoch生成器的部分结果
30 20220519024333
70 20220519024350

可以很明显的看出随着训练过程的进行,生成器的图像出现了明显的重复

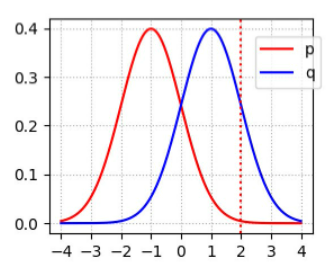
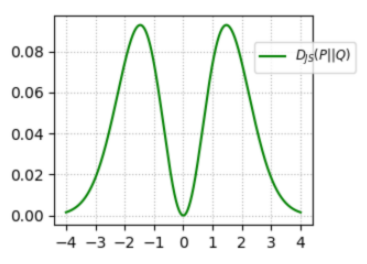
这也是KL散度所带来的问题.我们假设有如下两个正态分布,我们可以画出需要优化的方向,即JS散度的图像

其中p代表真实图像的分布,q代表生成的图像的分布

2022051819532920220518211729

当我们选取红线所在的位置(x=2),此时$p(x)\rightarrow0,q(x)>0$,此时对应的$D_{js}(p||q)$很大,同样的对称位置(x=-2)JS散度依然很高,也就是惩罚很高

这两种情况下的惩罚都是巨大的.导致生成器训练起来难度巨大

我们之前提到过训练生成器G的时候往往不使用 $\log(1-D(G(z)))$,因为它接近0,梯度很小,很难训练G

GAN的论文中也提出了一种改进做法是损失变为 $-\log(D(G(z)))$,这种技巧也被成为 - log D trick或者 the - log D alternative,在训练中确实有所帮助

但是这会带来另外的问题,这种情况下我们计算生成器G的梯度时

$$ \Delta\theta = \nabla_{\theta}E_{z\thicksim p(z)}[-\log D(g_{\theta}(z))] $$

根据前文的数学推导可以得出这个梯度可以转化为

$$ \Delta\theta = KL(P_g||P_{data})-2JS(P_{data}||P_g) $$

{% note info %} 这个等价最小化目标存在两个严重的问题。第一是它同时要最小化生成分布与真实分布的KL散度,却又要最大化两者的JS散度,一个要拉近,一个却要推远！这在直观上非常荒谬,在数值上则会导致梯度不稳定,这是后面那个JS散度项的毛病 {% endnote %}

即便是前面那个正常的KL散度项也有毛病,我们先把这种状况下的KL散度图画出来

那么对于KL散度的定义

$KL(p||q) = \int_x p(x)\log\frac{p(x)}{q(x)}dx$

$KL(q||p) = \int_x q(x)\log\frac{q(x)}{p(x)}dx$

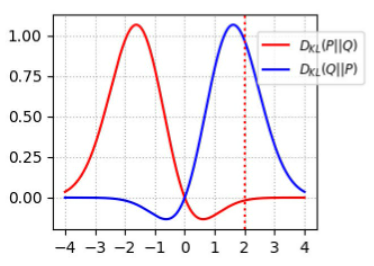
我们可以分别画出它们对应的图像,值得注意的是KL散度是非对称的,两个图像不相同,我们这里只需要关注$D_{kl}(Q||P)$红色的曲线即可

2022051819532920220518195922

换言之,$D_{kl}(Q||P)$对于上面两种错误的惩罚是不一样的

对于前文提到的两种情况:

第一种错误对应的是“生成器没能生成真实的样本”,惩罚微小,第二种错误对应的是“生成器生成了不真实的样本” ,惩罚巨大.

我们按照“人类正常的思绪”来看,“像的生成不了”和“能生成的不像”实际表达的都是“生成器烂”这一件事儿,但是KL散度却给出了截然相反的两种惩罚结果,一个“挠痒痒”和一个“往死打”

这一放一打之下,生成器宁可多生成一些重复但是很“安全”的样本,也不愿意去生成多样性的样本,因为那样一不小心就会产生第二种错误,得不偿失。这种现象就是大家常说的mode collapse

第一种错误对应的是缺乏多样性,第二种错误对应的是缺乏准确性

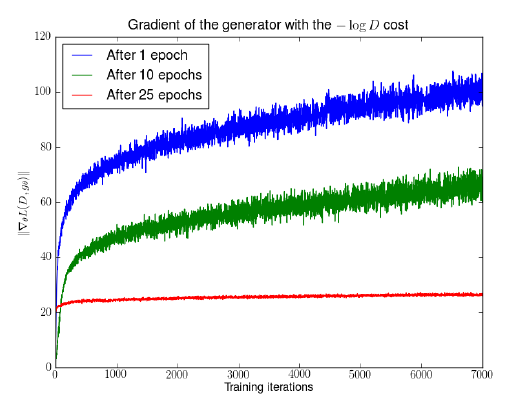
{% note info %} 除了上述的缺陷,该文还通过数学证明这种-logD的目标函数还存在梯度方差较大的缺陷,导致训练的不稳定。然后同样通过实验直观地验证了这个现象,如下图,在训练的早期（训练了1 epoch和训练了10 epochs）,梯度的方差很大,因此对应的曲线看起来比较粗,直到训练了25 epochs以后GAN收敛了才出现方差较小的梯度

可以看到随着判别器的训练,蓝色和绿色曲线中生成器的梯度迅速增长,说明梯度不稳定,红线对应的是DCGAN相对收敛的状态,梯度才比较稳定

v2-45ec2b5c75b83beaa5be3dea80122f2c_720w

{% endnote %}

zood