CacheLab

前言

本次实验是针对第六章Cache的内容,涉及到对于缓存替换策略的理解和具体代码的编写.

本次实验分为两个部分,Part A是编写一个缓存模拟器,Part B是优化矩阵变换

实验报告

下载valgrind

sudo apt install valgrind

下面这条指令会执行ls -l指令并且记录相应的内存访存时的信息

valgrind --log-fd=1 --tool=lackey -v --trace-mem=yes ls -l

注:这条指令会执行一小段时间,并且输出很多信息

在输出的信息之中,I表示 instruction load, L表示 data load, S 表示data store, M表示data modify,接着是一个64位地址和操作的字节数

Part A: Writing a Cache Simulator

Part A是实现一个简单的cache,模拟csim-ref的输入和输出格式,参数sEb也都是书中介绍过的

getopt使用方法

getopt方法解析

这里的代码实现思路参考CSAPP:Lab4-Cache Lab

由于只是模拟计算cache的miss hit eviction,并不需要真的保存数据,trace文件中也没有数据用于缓存,所以CacheLine没有定义缓存块B

CacheLine的标记位tag正常来说是可以通过64-b-s来计算的,但由于是变长用char*处理起来有些麻烦所以使用了unsigned long 一个64位无符号整数来简化处理

整个程序的执行过程大致思路是,首先通过argparser解析命令行参数,initCache根据s,E初始化一个Cache对象.simulate中visitCache函数是关键,根据s,b划分标记位,索引位,并且通过索引位(set_index)找到cache中的索引块

判断有效位,如果为1继续判断标记位.如果为0则认为是一个空块.这里的LRU算法的实现很精巧,最近被访问的lru设为1,在遍历的过程中每个块的lru++,evict块标记为所有块中lru值最大的,这样如果没有空块可以直接找到evict块进行一个lru替换

#include "cachelab.h"

#include <getopt.h>
#include <stdlib.h>
#include <unistd.h>
#include <stdio.h>
#include <math.h>

const char* usage = "Usage: %s [-hv] -s <s> -E <E> -b <b> -t <tracefile>\n";

int verbose = 0; //verbose flag
int s=-1;  //number of set index bits
int E=-1;  //number of lines per set
int b=-1;  //number of block bits
FILE* fp = NULL;

int hits = 0;
int misses = 0;
int evictions = 0;

#define HIT 1
#define MISS 2
#define EVICTION 3

typedef unsigned long uint64_t;

typedef struct {
    int valid;
    int lru;
    uint64_t tag;
} CacheLine;

typedef struct {
    // int E;
    CacheLine *cache_lines;
} CacheGroup;

typedef struct {
    // int S;
    CacheGroup *cache_groups;
} Cache;

void argparser(int argc, char* argv[]) {
    int opt;
    while ((opt = getopt(argc, argv, "hvs:E:b:t:")) != -1)
    {
        switch(opt)
        {
            case 'h':
                fprintf(stdout, usage, argv[0]);
                exit(1);
            case 'v':
                verbose = 1;
                break;
            case 's':
                s = atoi(optarg);
                break;
            case 'E':
                E = atoi(optarg);
                break;
            case 'b':
                b = atoi(optarg);
                break;
            case 't':
                fp = fopen(optarg, "r");
                break;
            default:
                fprintf(stdout, usage, argv[0]);
                exit(1);
        }
    }
    if (s == -1 || E == -1 || b == -1) {
        printf("s E b are required\n");
        exit(1);
    }
}

Cache* initCache() {
    // 根据s,E初始化cache
    int S = 1 << s;
    Cache *cache = malloc(sizeof(Cache));
    cache->cache_groups = calloc(S,sizeof(CacheGroup));
    for(int i=0;i<S;i++) {
        cache->cache_groups[i].cache_lines = (CacheLine*)calloc(E,sizeof(CacheLine));
    }
    return cache;
}

int visitCache(Cache *cache, uint64_t address) {

    uint64_t set_index = address >> b & ((1 << s) - 1);
    uint64_t tag = address >> (b+s);
    // printf("address = %lx, set_index = %lx, tag = %lx\n",address,set_index,tag);
    CacheGroup cache_group = cache->cache_groups[set_index];
    int evict = 0;
    int empty = -1;
    for(int i=0;i<E;i++) {
        if (cache_group.cache_lines[i].valid) {
            if (cache_group.cache_lines[i].tag == tag) {
                hits++;
                cache_group.cache_lines[i].lru = 1;
                return HIT;
            }
            cache_group.cache_lines[i].lru++;
            if (cache_group.cache_lines[evict].lru <= cache_group.cache_lines[i].lru) {
                evict = i;
            }
        } else {
            empty = i;
        }
    }
    misses++;
    if (empty != -1) {
        cache_group.cache_lines[empty].valid = 1;
        cache_group.cache_lines[empty].tag = tag;
        cache_group.cache_lines[empty].lru = 1;
        return MISS;
    } else {
        cache_group.cache_lines[evict].tag = tag;
        cache_group.cache_lines[evict].lru = 1;
        evictions++;
        return EVICTION;
    }
}

void simulate(Cache *cache) {

    char buf[30];
    char operation;
    uint64_t address;
    int size;
    int result;
    while (fgets(buf, sizeof(buf), fp) != NULL) {
        if (buf[0] == 'I') continue;
        sscanf(buf, " %c %lx,%d", &operation, &address, &size);
        result = visitCache(cache, address);
        if (operation == 'M') hits++;
        if (verbose) {
            switch (result) {
                case HIT:
                    printf("%c %lx,%d hit\n", operation, address, size);
                    break;
                case MISS:
                    printf("%c %lx,%d miss\n", operation, address, size);
                    break;
                case EVICTION:
                    printf("%c %lx,%d miss eviction\n", operation, address, size);
                    break;
                default:
                    fprintf(stdout, "unknown cache behave");
                    exit(1);
            }
        }
    }
    fclose(fp);
}

void freeCache(Cache* cache) {
    int S = 1<<s;
    for(int i=0;i<S;i++) {
        free(cache->cache_groups[i].cache_lines);
    }
    free(cache->cache_groups);
    free(cache);
}

int main(int argc, char **argv)
{
    argparser(argc,argv);
    Cache *cache = initCache();
    simulate(cache);
    freeCache(cache);
    printSummary(hits, misses, evictions);
    return 0;
}

$ make
$ ./test-csim
                        Your simulator     Reference simulator
Points (s,E,b)    Hits  Misses  Evicts    Hits  Misses  Evicts
     3 (1,1,1)       9       8       6       9       8       6  traces/yi2.trace
     3 (4,2,4)       4       5       2       4       5       2  traces/yi.trace
     3 (2,1,4)       2       3       1       2       3       1  traces/dave.trace
     3 (2,1,3)     167      71      67     167      71      67  traces/trans.trace
     3 (2,2,3)     201      37      29     201      37      29  traces/trans.trace
     3 (2,4,3)     212      26      10     212      26      10  traces/trans.trace
     3 (5,1,5)     231       7       0     231       7       0  traces/trans.trace
     6 (5,1,5)  265189   21775   21743  265189   21775   21743  traces/long.trace
    27
TEST_CSIM_RESULTS=27

这里要补充一点的是,所有测试用例中的缓存块大小B都大于等于trace中的B,所以不存在访问一个连续单元的长度大于一个缓存块导致需要连续访存的情况.这种情况要复杂一些,可能还需要判断B大小划分成几块来计算.

Part B: Optimizing Matrix Transpose

PartB 的任务是利用缓存实现对矩阵转置的优化,缓存的规格是s=5,E=1,b=5,也就是32组每组一行保存32B数据.由于矩阵的数据类型是int(4字节),所以缓存每行可以保存8个int矩阵单元

需要转置的矩阵的大小有三组,分别是32x32, 64x64, 61x67, 我们需要完成的函数是tran.s中的transpose_submit

除此之外文档中还有其他的要求

• 一共只准使用不超过 12 个 int 类型局部变量

• 不能用递归

• 不能改变A数组中的值

• 不能定义新的数组也不能用 malloc 函数开辟空间

• cache miss 的次数尽可能少

trans.c中使用registerTransFunction将转置函数注册进去,我们可以直接在transpose_submit中编写代码,根据M的不同输入值判断

char transpose_submit_desc[] = "Transpose submission";
void transpose_submit(int M, int N, int A[N][M], int B[M][N])
{
    if (M == 32) {
        //
    } else if (M == 64) {
        //
    } else {
        //
    }
}

也可以新建函数,然后手动将其注册进去

char transpose_32x32[] = "Transpose 32x32";
void transpose_submit_32x32(int M, int N, int A[N][M], int B[M][N]) {
    //
}

void registerFunctions()
{
    /* Register your solution function */
    registerTransFunction(transpose_submit, transpose_submit_desc);
    /* Register any additional transpose functions */
    registerTransFunction(trans, trans_desc);
    registerTransFunction(transpose_submit_32x32,transpose_32x32);
}

本文采用第一种方式,即if判断

分块技术

分块技术(block)是一种非常有效的提高缓存命中,局部性的方法,尽量在每一个块中充分利用缓存保存更多的数据

32x32

由于本题中基础cache结构确定,一共32组,每组可以保存8个int,所以我们先使用一个8x8的分块

void transpose_submit(int M, int N, int A[N][M], int B[M][N])
{
    if (M == 32) {
        // int i,j,k,l;
        for (int i=0;i<N;i+=8) {
            for (int j=0;j<M;j+=8) {
                for(int k=i;k<i+8;k++) {
                    for(int l=j;l<j+8;l++) {
                        B[l][k] = A[k][l];
                    }
                }
            }
        }
    }
}

测试结果如下,缓存misses次数为343,并没有小于300次拿到满分

$ ./test-trans -M 32 -N 32

Function 0 (1 total)
Step 1: Validating and generating memory traces
Step 2: Evaluating performance (s=5, E=1, b=5)
func 0 (Transpose submission): hits:1710, misses:343, evictions:311

Summary for official submission (func 0): correctness=1 misses=343

TEST_TRANS_RESULTS=1:343

我们可以将一个32x32的矩阵看作16(4x4)个8x8组成的小矩阵

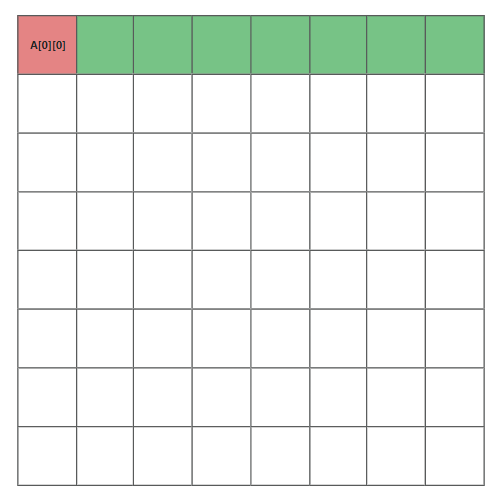
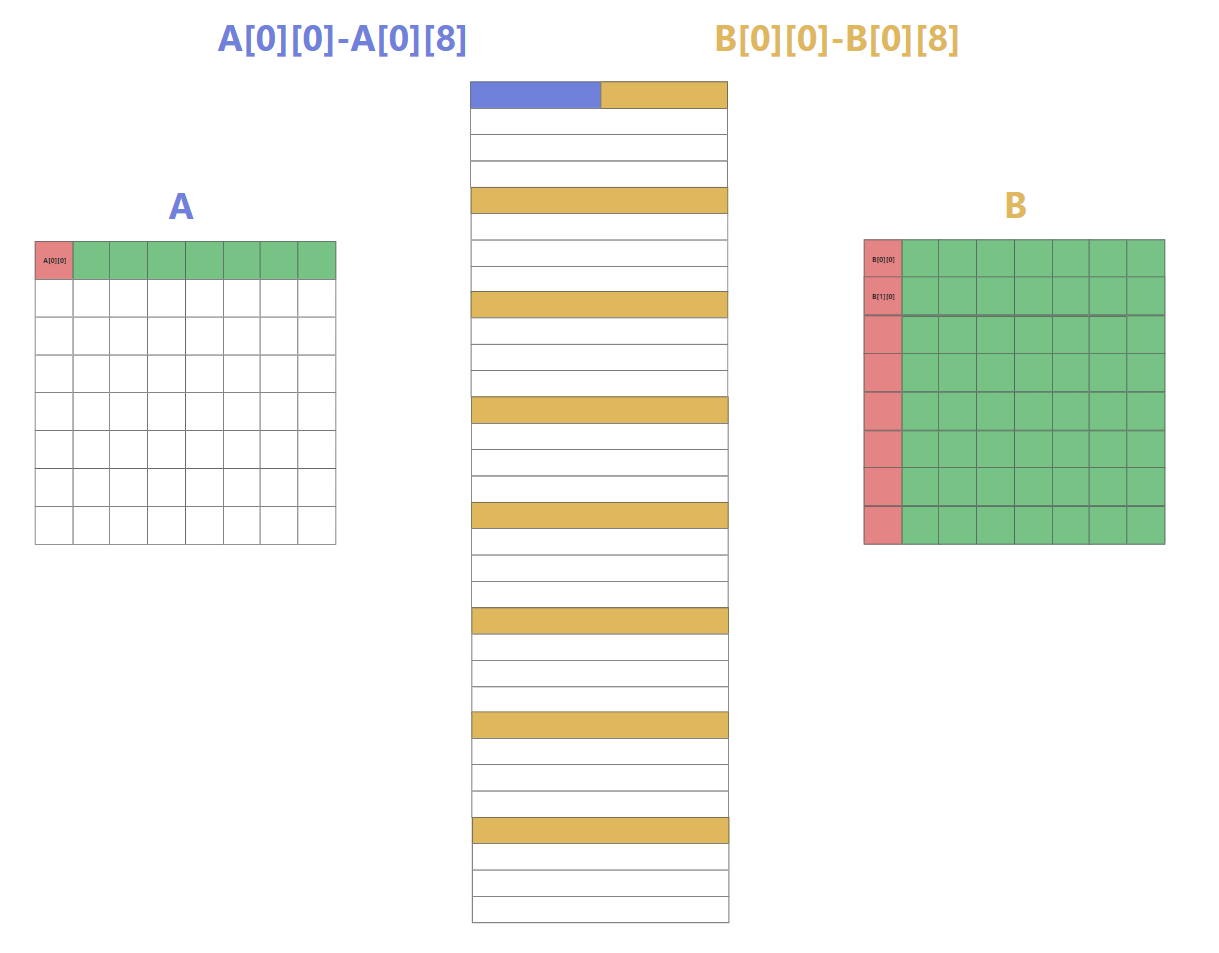
当访问A[0][0]的时候,由于缓存b=5,所以实际上一次性取出了8个元素,A[0][0]-A[0][8]

在每一个8x8block的循环过程中,A的访问每一行第一次访问时miss一次,之后的7次全部hit.一共8行,miss8次

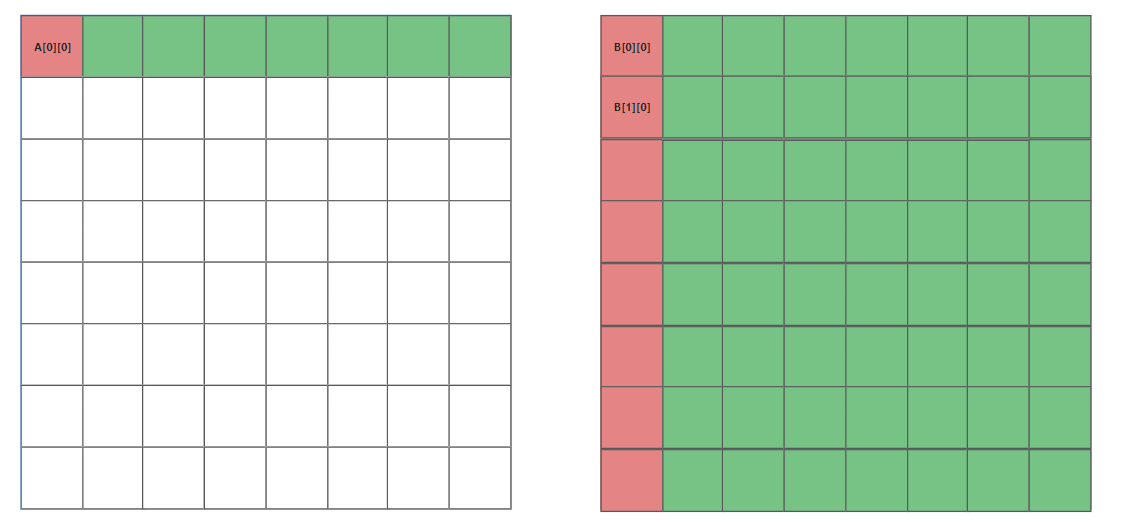
由于进行转置时需要对B矩阵进行赋值操作B[i][j] = A[j][i],在向内存中写数据时,可能会发生以下几种情况

• 写命中:
  • write-through:直接写内存
  • write-back:先写Cache,当该行被替换时再写内存.此时需要一个额外的dirty位

• 写不命中
  • write-allocate:将内存数据读入Cache中,再写Cache
  • no-write-allocate:直接写内存

本题的操作方式是写命中与否都会使用Cache缓存B的值,所以第一次读取B数组的值的时候也会产生一次miss

A是横向读取,后7个不会产生miss. B是纵向读取,所以第一次虽然是读取第一列B[i][0],8次miss,但实际上将整个B数组全部写入了缓存中,之后的第二列第三列B读取就可以直接在缓存中hit了

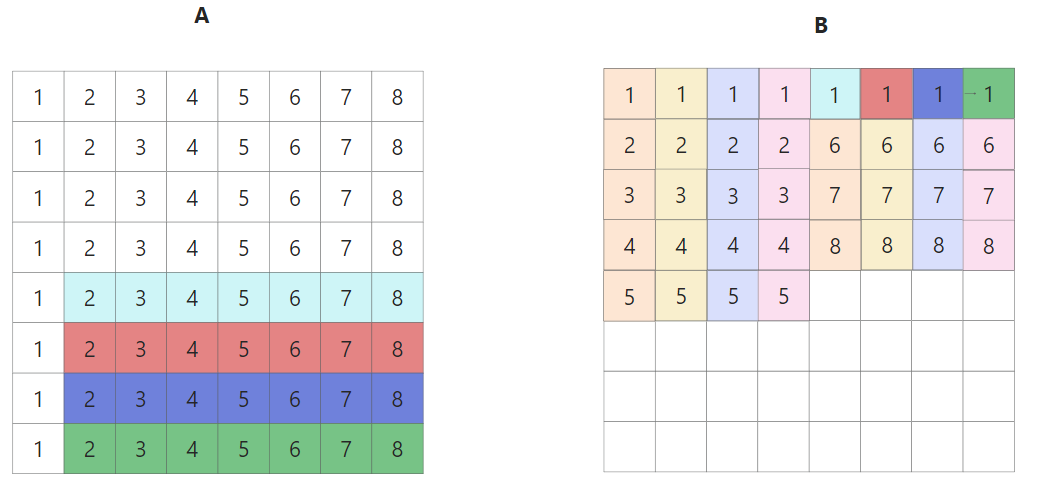
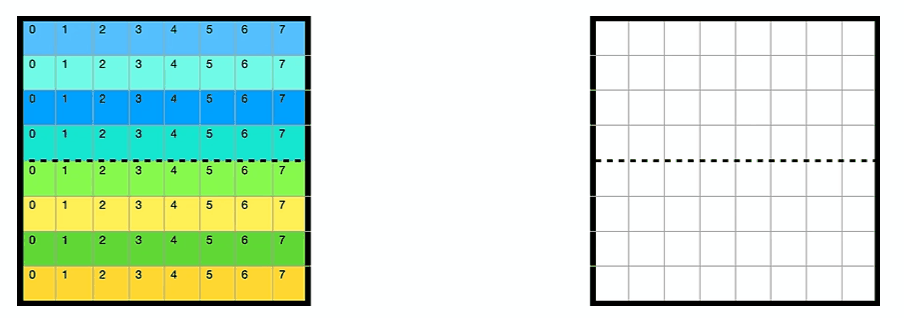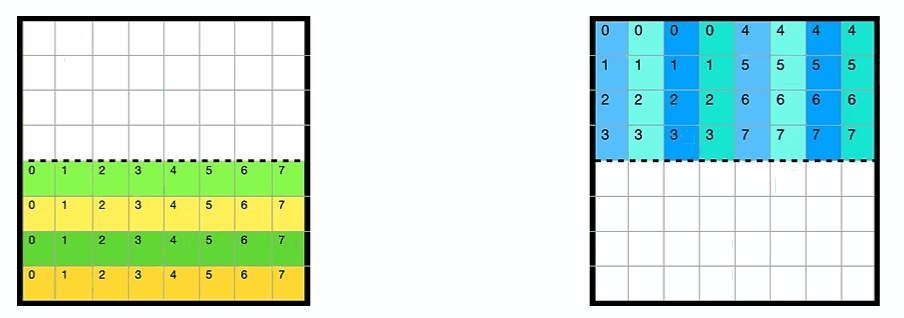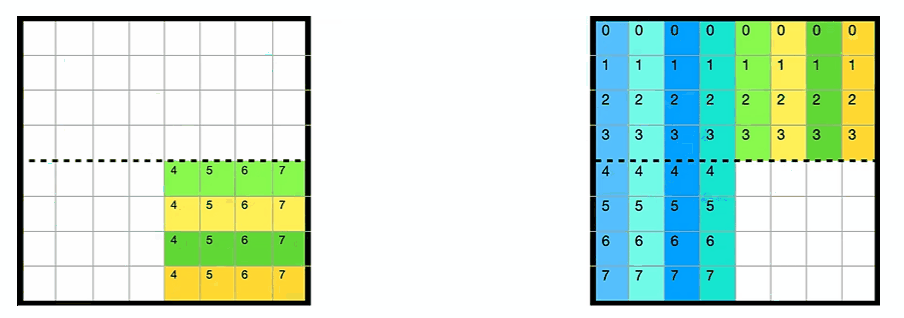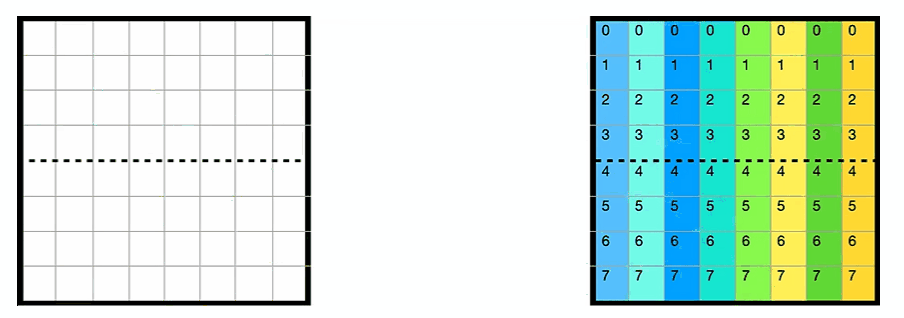
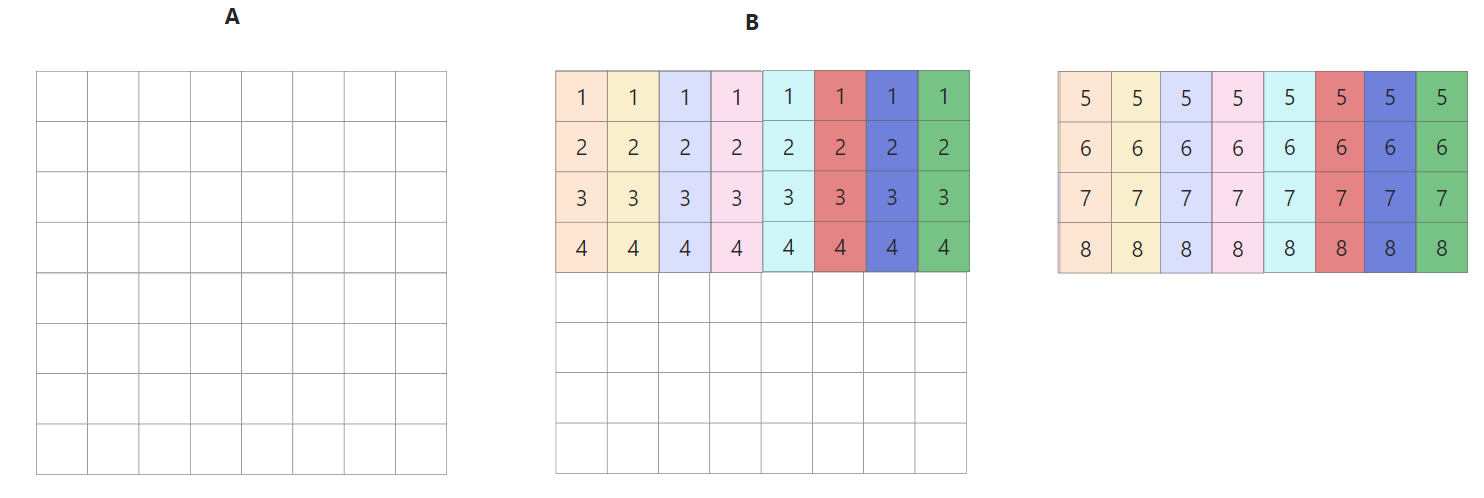
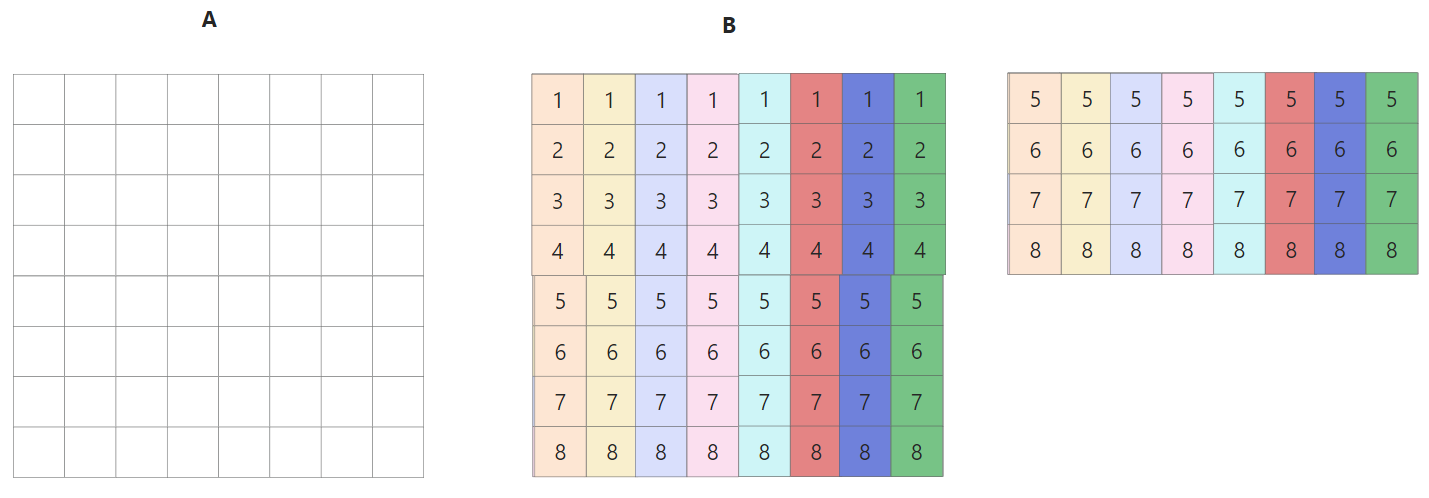
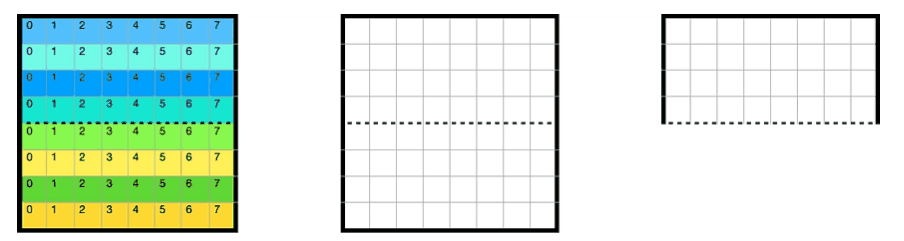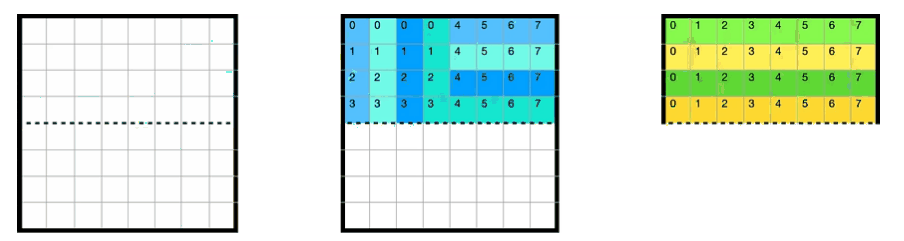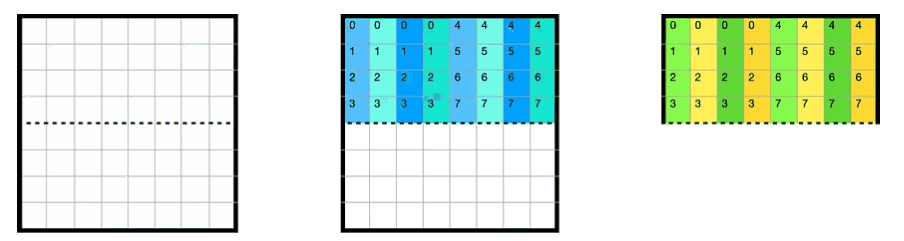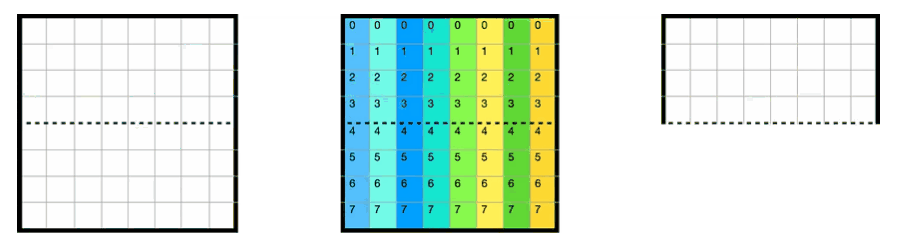
于此同时,缓存cache的情况如下所示,A的第一行被缓存在cache的第一行(以下简称cache[0]),B的每一行被缓存在间隔为4的位置(因为全矩阵32x32,每一大行4个小block)

每个block中每一行映射到cache[4x]的位置,如下图所示

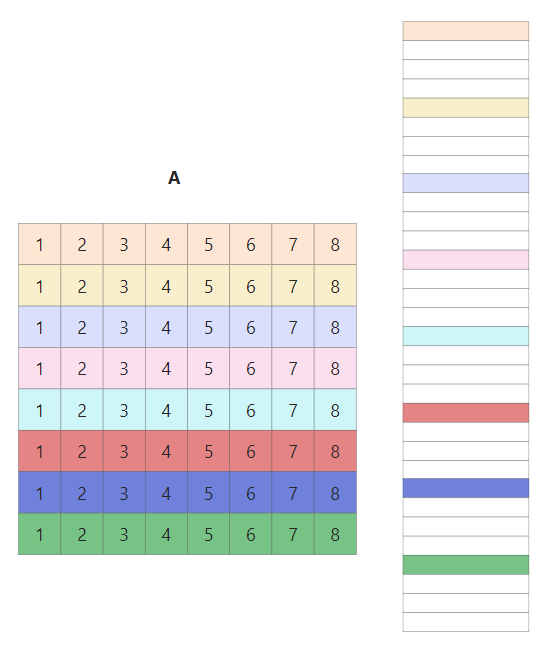
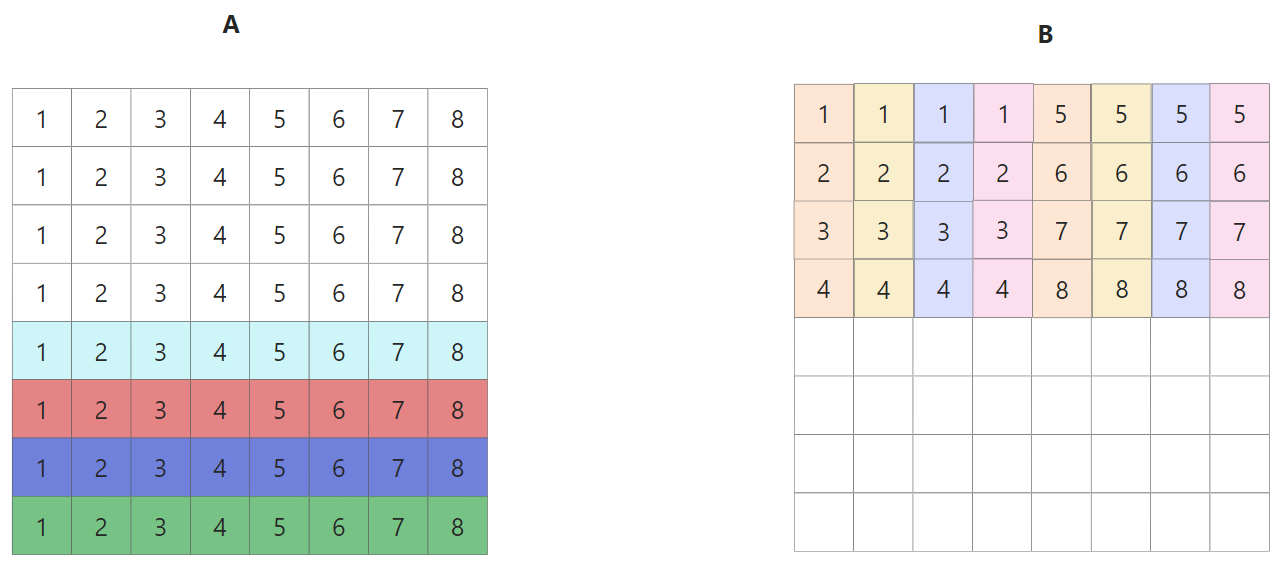
上述情况是对于第一个小block来说的,全部16个block的遍历顺序如下图所示,由于整个矩阵是32x32.且cache为32组. 以这种方式遍历的好处是1234遍历的时候互不干涉,block里面的每一行映射到cache[4x]的行中

其实block遍历的顺序并无影响,这里只是演示一下内存地址和cache映射的关系

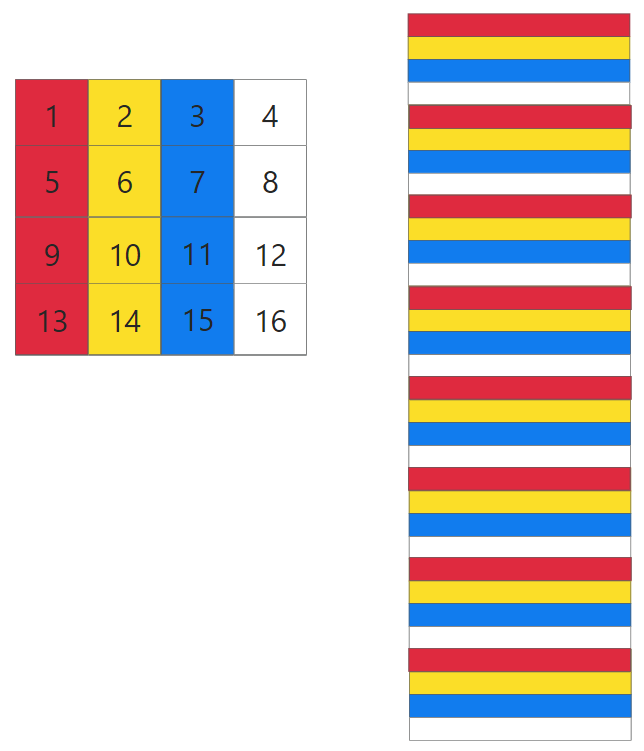
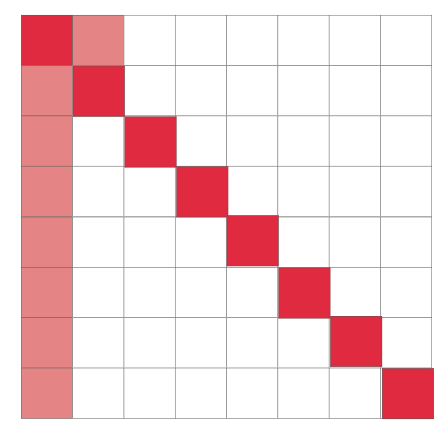
当不是对角线上的block,此时AB两个矩阵映射的不是一个颜色的区域cache,所以一定不会出现冲突. 但是对于对角线上的block,当我们尝试执行B[0][0] = A[0][0]的时候,首先读取A[0][0],cache[0] miss,将A[0][0]-A[0][8]加载到cache[0]中; 然后读取B[0],cache[0] miss,将B[0][0]-B[0][8]加载到cache[0],此时覆盖掉原先A的缓存了, 接着A[0][1]再次miss,这样就多造成了两次 miss

同时我们发现对角线上的元素A[i][i]都存在这个问题

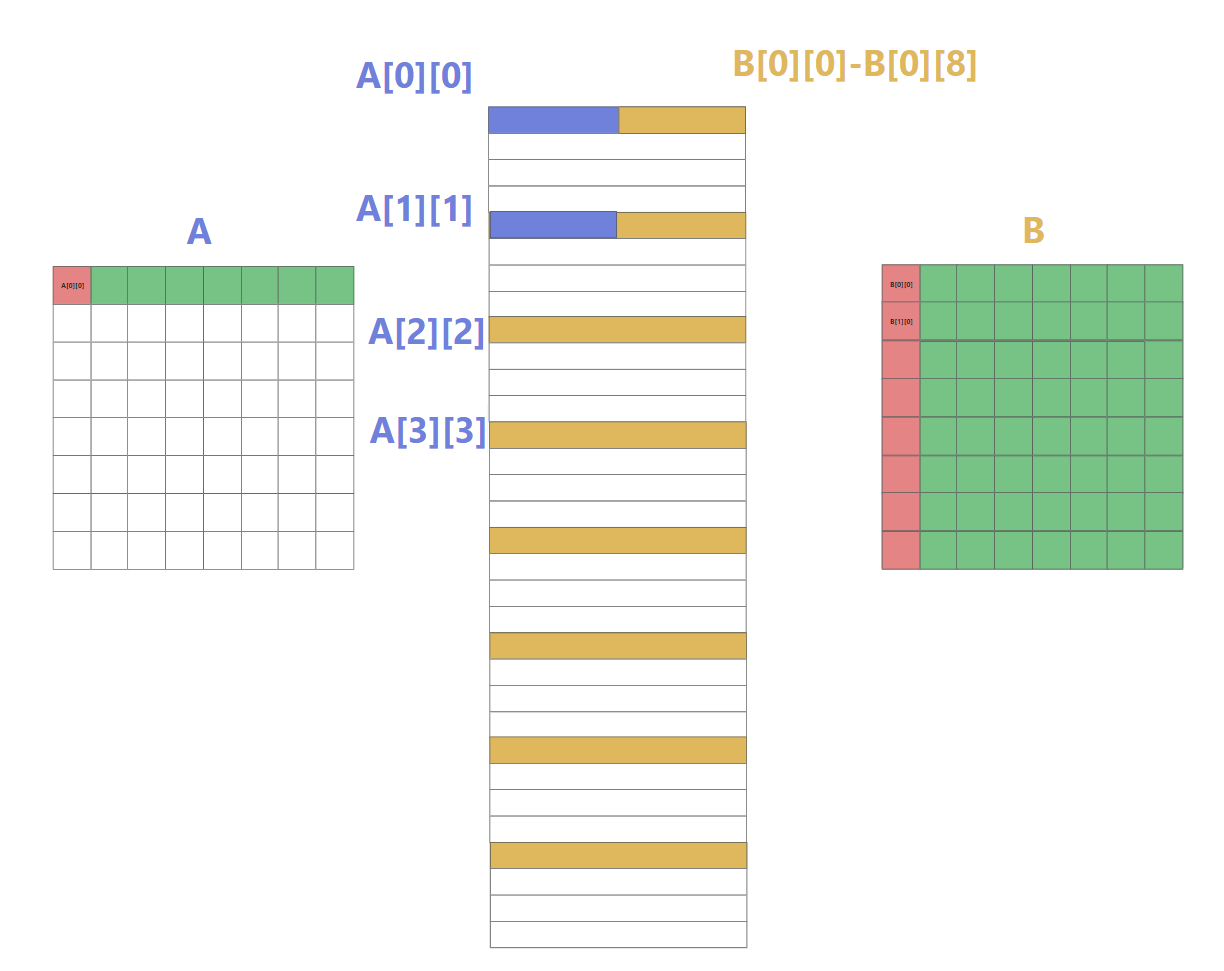
所以为了解决这个问题,我们可以利用8个局部变量将每次读入的A[0][0]-A[0][8]的每个值存起来,这样即使B[0][0]-B[0][8]覆盖掉cache[0]后也可以直接拿到A该行剩余的数组元素了

这里有一个小点要说明一下,实际上这种利用局部变量保存值的做法相当于多次连续调用cache把值保存到栈里,栈在内存中其访问速度比cache慢,这点上来说虽然减少了cache miss,但或许还需要判断一下速度到底是多次缓存抖动快还是内存访问快,我也不是很确定. 不过从本实验来说cache miss次数是第一重要

void transpose_submit(int M, int N, int A[N][M], int B[M][N])
{
    if (M == 32) {
        int i, j, k;
        int t0, t1, t2, t3, t4, t5, t6, t7;
        for (i = 0; i < N; i += 8) {
            for (j = 0; j < M; j += 8) {
                for (k = i; k < i+8; k++) {
                    t0 = A[k][j];
                    t1 = A[k][j + 1];
                    t2 = A[k][j + 2];
                    t3 = A[k][j + 3];
                    t4 = A[k][j + 4];
                    t5 = A[k][j + 5];
                    t6 = A[k][j + 6];
                    t7 = A[k][j + 7];
                    B[j][k] = t0;
                    B[j + 1][k] = t1;
                    B[j + 2][k] = t2;
                    B[j + 3][k] = t3;
                    B[j + 4][k] = t4;
                    B[j + 5][k] = t5;
                    B[j + 6][k] = t6;
                    B[j + 7][k] = t7;
                }
            }
        }
    }
}

$ ./test-trans -M 32 -N 32

Function 0 (1 total)
Step 1: Validating and generating memory traces
Step 2: Evaluating performance (s=5, E=1, b=5)
func 0 (Transpose submission): hits:1766, misses:287, evictions:255

Summary for official submission (func 0): correctness=1 misses=287

TEST_TRANS_RESULTS=1:287

此时我们发现次数变为了287次,已经得到第一题的满分了. 那么本题最优次数应该是多少呢?

对于8x8的分块来说,一共16个小矩阵,AB在cache中各自至少有8次miss,所以理论上最佳miss次数为(8+8)x16=256

如果不是8x8的分组,4x4的话miss次数为(4+4)x(8x8),16x16的话每个块内由于cache行只能保存8个int,所以每个数组会出现32次miss,总miss为(32+32)x4,,但是由于cache只有32组,不可能同时保存AB两个矩阵的行(32+32>32),所以必定出现cache冲突的替换,反而增大miss

那么多出来的这些miss是为什么呢? 实际上即使我们使用临时变量保存仍然会出现替换造成的miss. B在第一列的时候将所有的数组元素都加载到cache[4x]中了,其后A每下移一行,在对角线处都会替换一次cache[4x]的位置,如果能把 B 中的对角线元素命中的话,就可以达到理论上的 256 次 miss

处理冲突不命中,就是要处理重复的加载. 对于AB重复访问的情况

• 在 A 访问第二行之前不让 B 访问第二行

• 在 A 访问第二行之后不让 B 访问第二行

后者不可能做到因为B一定是要写入的,所以我们考虑延迟B访问第二行的时间,也就是处理第一列的时候. 所以我们换一个思路,能否等 A 的下一行的元素访问完了再转置?

因为自由变量是有限的(不然直接256个变量上去了),所以我们可以将 A 的元素暂存在 B 的第一行,等到下一行读到变量里再访问 B 的下一行. 当i==j的时候手动交换8x8区域内的元素,利用八个变量交替读取A的每一行,并保存到B的行中,然后在每一列中做对应的转置处理

void transpose_submit(int M, int N, int A[N][M], int B[M][N])
{
    if (M == 32) {
        int i, j, k, l;
        int t0, t1, t2, t3, t4, t5, t6, t7;
        for (i = 0; i < N; i += 8) {
            for (j = 0; j < M; j += 8) {
                if (i != j) {
                    for (k = i; k < i + 8; k++) {
                        for (l = j; l < j + 8; l++) {
                            B[l][k] = A[k][l];
                        }
                    }
                } else {
                    for (k = i; k < i + 8; k++) {
                        t0 = A[k][j];
                        t1 = A[k][j + 1];
                        t2 = A[k][j + 2];
                        t3 = A[k][j + 3];
                        t4 = A[k][j + 4];
                        t5 = A[k][j + 5];
                        t6 = A[k][j + 6];
                        t7 = A[k][j + 7];
                        B[k][j] = t0;
                        B[k][j + 1] = t1;
                        B[k][j + 2] = t2;
                        B[k][j + 3] = t3;
                        B[k][j + 4] = t4;
                        B[k][j + 5] = t5;
                        B[k][j + 6] = t6;
                        B[k][j + 7] = t7;
                    }
                    for (k = i; k < i + 8; k++) {
                        for (l = j + (k - i + 1); l < j + 8; l++) {
                            if (k != l) {
                                t0 = B[k][l];
                                B[k][l] = B[l][k];
                                B[l][k] = t0;
                            }
                        }
                    }
                }
            }
        }
    }
}

$ ./test-trans -M 32 -N 32

Function 0 (1 total)
Step 1: Validating and generating memory traces
Step 2: Evaluating performance (s=5, E=1, b=5)
func 0 (Transpose submission): hits:2242, misses:259, evictions:227

Summary for official submission (func 0): correctness=1 misses=259

TEST_TRANS_RESULTS=1:259

最后结果是259,多了3次与转置无关的操作,结果正确

64x64

对于64的数组如果我们依然按照32的思路采用8x8的方式如法炮制,我们会发现block内就会出现冲突

因为之前矩阵长度为32,计算得出8x8划分的话A矩阵中的8行刚好被对应映射到cache[4x]的位置,而64的话对应被映射到cache[8x]的位置,所以在一个块内,前四行和后四行甚至出现了冲突!

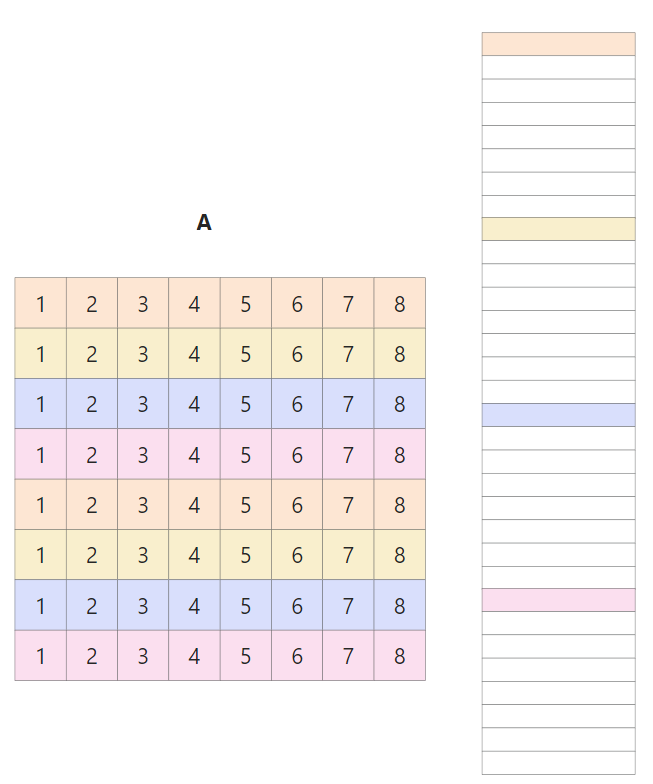
一种直观的想法是仅仅将数组大小改为4x4

if (M == 32) {
    // ...
}
else if (M == 64) {
    int i, j, k, l;
    int t0, t1, t2, t3;
    for (i = 0; i < N; i += 4) {
        for (j = 0; j < M; j += 4) {
            if (i != j) {
                for (k = i; k < i + 4; k++) {
                    for (l = j; l < j + 4; l++) {
                        B[l][k] = A[k][l];
                    }
                }
            } else {
                for (k = i; k < i + 4; k++) {
                    t0 = A[k][j];
                    t1 = A[k][j + 1];
                    t2 = A[k][j + 2];
                    t3 = A[k][j + 3];
                    B[k][j] = t0;
                    B[k][j + 1] = t1;
                    B[k][j + 2] = t2;
                    B[k][j + 3] = t3;
                }
                for (k = i; k < i + 4; k++) {
                    for (l = j + (k - i + 1); l < j + 4; l++) {
                        if (k != l) {
                            t0 = B[k][l];
                            B[k][l] = B[l][k];
                            B[l][k] = t0;
                        }
                    }
                }
            }
        }
    }
}

$ ./test-trans -M 64 -N 64

Function 0 (1 total)
Step 1: Validating and generating memory traces
Step 2: Evaluating performance (s=5, E=1, b=5)
func 0 (Transpose submission): hits:6834, misses:1747, evictions:1715

Summary for official submission (func 0): correctness=1 misses=1747

TEST_TRANS_RESULTS=1:1747

我们可以看到miss为1747,但实际上理论最优值应该是2x64x(64/8) = 1024

所以我们还是需要考虑使用8x8的block,然后考虑移动修改取出A的时机和B中保存和修改的顺序以及位置,这里直接讲解一下一种比较巧妙的方式

由于block中前四行和后四行存在冲突,所以前四行和后四行的处理不相同. 同时8x8分块一共是8x8个block,每个block对应映射到cache的位置如下所示

1. 非对角线上的block

   这种情况比较简单,因为不存在对角线那种AB映射到一个cache的情况,AB两个块是按照对角线对称的位置,AB内部会出现冲突,但是AB之间一定不会出现cache冲突

   第一步, 将A前四行拆分为两列映射到B中,转置, 4miss + 4miss

   

   

   

   

   使用这种方式映射的原因是64x64的矩阵映射的cache为cache[8x],所以如果映射到下半区(下四行)就会导致cache冲突. 通过这种方式A每次读取一行miss一次,一共4次miss,B第一次写入1-4列的时候产生4次miss,之后都是0miss

   第二步,将B右上移动到B左下,转置; 将A左下移动到B右上,转置, 4 miss + 4 miss

   

   这里先将B[0][4]-B[0][7]的元素移动到左下,1次miss. 然后将A中第一列剩余元素移动到[0][4]-B[0][7]的位置,4次miss. 接着左下部分全部移动完毕后如下所示

   

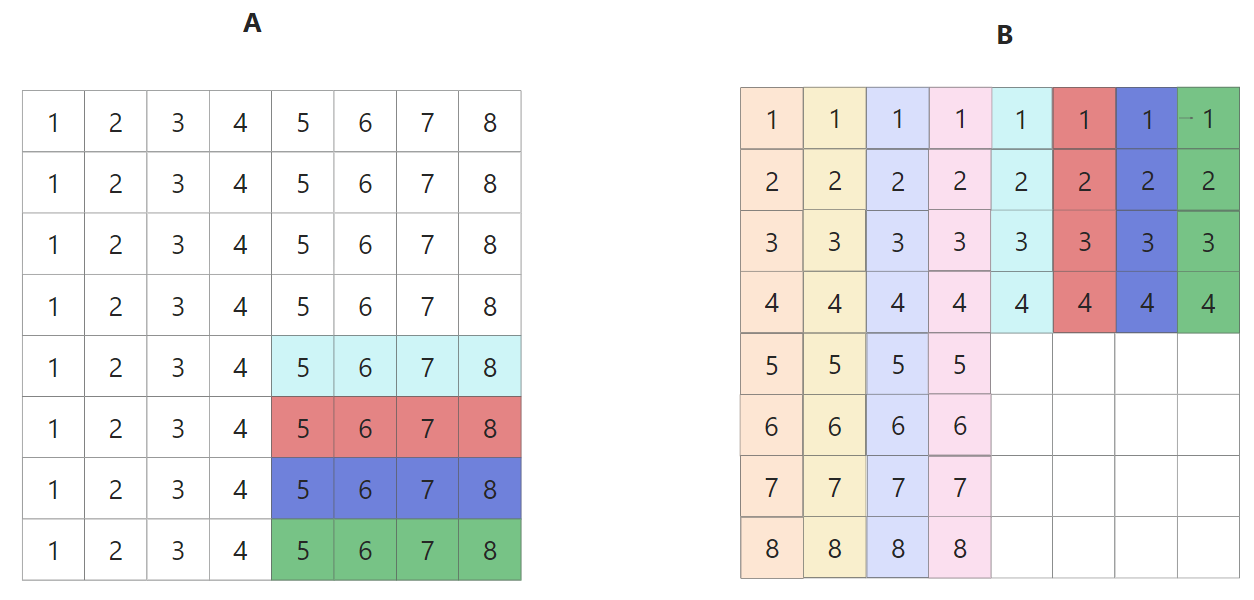
   其中A只在第一次读一列的时候产生4次miss,B每次更新一行,连续4次1 miss

   第三步,将A矩阵右下移动到B矩阵右下,转置, 0miss + 0miss

   

   

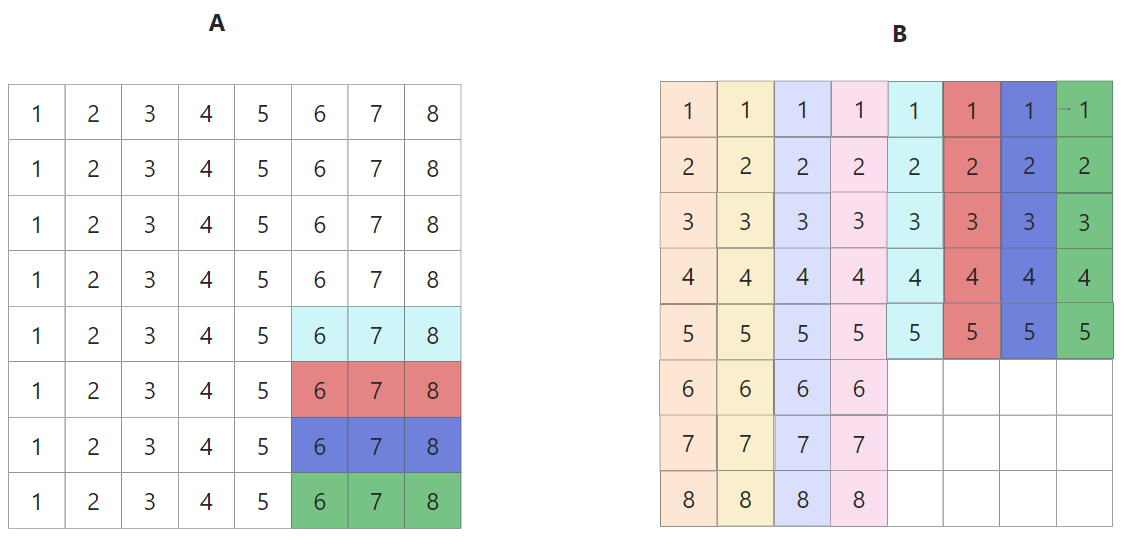
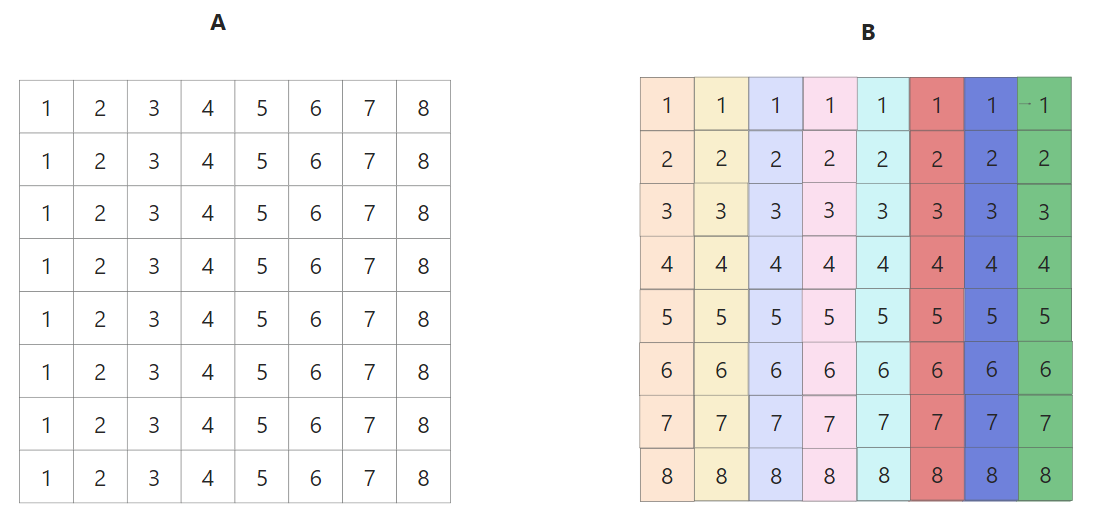
   至此,非对角线上的block更新完毕, 一共A 8次miss, B 8次miss,最好情况16miss,完整动图如下

   

   gif原图来自知乎文章

2. 对角线block

   对于对角线上的block,此时AB映射到同一个cache的位置,此时仅仅利用一个8x8的block冲突太多了,我们还需要一个借用的块

   初始状态为A,B和一个借用的块

   

   第一步,将A下半部分复制到借用矩阵.4miss + 4miss

   

   第二步,将A上半部分移动到B矩阵上半部分,4miss + 4miss

   

   第三步,借用矩阵的两个4x4分别转置,0 miss + 0 miss

   

   第四步,B矩阵的两个4x4分别转置,0 miss + 0 miss

   

   第五步,交换B矩阵右上和借用矩阵左上,0 miss + 0 miss

   

   第六步,将借用矩阵复制到B矩阵下方,0miss + 4miss

   

   一共A 8miss, B12miss, 共20miss

   这里的借用矩阵位置十分巧妙,借用矩阵是借用B中的其他矩阵,我们首先处理对角线block,此时将部分数据保存在借用矩阵中,虽然这里B为12miss比非对角线block多出来了4miss,但是由于这里使用了借用矩阵,所以如果下一个非对角线block处理时第一步B就会少4miss,相当于借用到这里的4miss,综合下来没有多miss

   对于第一行的对角线block,其借用矩阵是后一个,其他行都是第一个,这样当我们以j,i的顺序遍历A矩阵,B矩阵以i,j的方式更新,优先处理对角矩阵,然后从每行开头处理非对角矩阵,总miss 16x64=1024

   

   完整动图如下

   

if (M == 32) {
    // ...
}
else if (M == 64) {
  int i, j, k, l;
  int a0, a1, a2, a3, a4, a5, a6, a7;
  // 优先处理对角线block
  for (j = 0; j < N; j += 8) {
      // 对于第一行的block,借用矩阵选择第一行第二个block
      // 其余都选择每一行的第一个block
      if (j == 0)
          i = 8;
      else
          i = 0;
      // 1. 将A矩阵下方4x8移动到借用矩阵位置 - 上半部分
      for (k = j; k < j + 4; ++k) {
          a0 = A[k + 4][j + 0];
          a1 = A[k + 4][j + 1];
          a2 = A[k + 4][j + 2];
          a3 = A[k + 4][j + 3];
          a4 = A[k + 4][j + 4];
          a5 = A[k + 4][j + 5];
          a6 = A[k + 4][j + 6];
          a7 = A[k + 4][j + 7];
          B[k][i + 0] = a0;
          B[k][i + 1] = a1;
          B[k][i + 2] = a2;
          B[k][i + 3] = a3;
          B[k][i + 4] = a4;
          B[k][i + 5] = a5;
          B[k][i + 6] = a6;
          B[k][i + 7] = a7;
      }
      // 2. 借用矩阵内部两个4x4转置
      for (k = 0; k < 4; ++k) {
          for (l = k + 1; l < 4; ++l) {
              a0 = B[j + k][i + l];
              B[j + k][i + l] = B[j + l][i + k];
              B[j + l][i + k] = a0;
              a0 = B[j + k][i + l + 4];
              B[j + k][i + l + 4] = B[j + l][i + k + 4];
              B[j + l][i + k + 4] = a0;
          }
      }
      // 3. 将A上方4x8移动到B上方
      for (k = j; k < j + 4; ++k) {
          a0 = A[k][j + 0];
          a1 = A[k][j + 1];
          a2 = A[k][j + 2];
          a3 = A[k][j + 3];
          a4 = A[k][j + 4];
          a5 = A[k][j + 5];
          a6 = A[k][j + 6];
          a7 = A[k][j + 7];
          B[k][j + 0] = a0;
          B[k][j + 1] = a1;
          B[k][j + 2] = a2;
          B[k][j + 3] = a3;
          B[k][j + 4] = a4;
          B[k][j + 5] = a5;
          B[k][j + 6] = a6;
          B[k][j + 7] = a7;
      }
      // 4. B矩阵上方两个4x4转置
      for (k = j; k < j + 4; ++k) {
          for (l = k + 1; l < j + 4; ++l) {
              a0 = B[k][l];
              B[k][l] = B[l][k];
              B[l][k] = a0;
              a0 = B[k][l + 4];
              B[k][l + 4] = B[l][k + 4];
              B[l][k + 4] = a0;
          }
      }
      // 5. B矩阵的右上和转置矩阵的左上交换
      for (k = 0; k < 4; ++k) {
          a0 = B[j + k][j + 4];
          a1 = B[j + k][j + 5];
          a2 = B[j + k][j + 6];
          a3 = B[j + k][j + 7];
          B[j + k][j + 4] = B[j + k][i + 0];
          B[j + k][j + 5] = B[j + k][i + 1];
          B[j + k][j + 6] = B[j + k][i + 2];
          B[j + k][j + 7] = B[j + k][i + 3];
          B[j + k][i + 0] = a0;
          B[j + k][i + 1] = a1;
          B[j + k][i + 2] = a2;
          B[j + k][i + 3] = a3;
      }
      // 6. 将借用矩阵移动到B矩阵下方
      for (k = 0; k < 4; ++k) {
          B[j + k + 4][j + 0] = B[j + k][i + 0];
          B[j + k + 4][j + 1] = B[j + k][i + 1];
          B[j + k + 4][j + 2] = B[j + k][i + 2];
          B[j + k + 4][j + 3] = B[j + k][i + 3];
          B[j + k + 4][j + 4] = B[j + k][i + 4];
          B[j + k + 4][j + 5] = B[j + k][i + 5];
          B[j + k + 4][j + 6] = B[j + k][i + 6];
          B[j + k + 4][j + 7] = B[j + k][i + 7];
      }
      // 处理非对角线block
      for (i = 0; i < M; i += 8) {
          if (i == j) {
              continue;
          } else {
              // 1. 将A矩阵上半部分移动到B上半部分
              //    分为两块 分别转置
              for (k = i; k < i + 4; ++k) {
                  a0 = A[k][j + 0];
                  a1 = A[k][j + 1];
                  a2 = A[k][j + 2];
                  a3 = A[k][j + 3];
                  a4 = A[k][j + 4];
                  a5 = A[k][j + 5];
                  a6 = A[k][j + 6];
                  a7 = A[k][j + 7];
                  B[j + 0][k] = a0;
                  B[j + 1][k] = a1;
                  B[j + 2][k] = a2;
                  B[j + 3][k] = a3;
                  B[j + 0][k + 4] = a4;
                  B[j + 1][k + 4] = a5;
                  B[j + 2][k + 4] = a6;
                  B[j + 3][k + 4] = a7;
              }
              // 2. B矩阵右上部分移动到B矩阵左下,转置
              //    A矩阵左下部分移动到B矩阵右上,转置
              for (l = j; l < j + 4; ++l) {
                  a0 = A[i + 4][l];
                  a1 = A[i + 5][l];
                  a2 = A[i + 6][l];
                  a3 = A[i + 7][l];
                  a4 = B[l][i + 4];
                  a5 = B[l][i + 5];
                  a6 = B[l][i + 6];
                  a7 = B[l][i + 7];
                  B[l][i + 4] = a0;
                  B[l][i + 5] = a1;
                  B[l][i + 6] = a2;
                  B[l][i + 7] = a3;
                  B[l + 4][i + 0] = a4;
                  B[l + 4][i + 1] = a5;
                  B[l + 4][i + 2] = a6;
                  B[l + 4][i + 3] = a7;
              }
              // 3. A矩阵右下部分移动到B矩阵右下,转置
              for (k = i + 4; k < i + 8; ++k) {
                  a0 = A[k][j + 4];
                  a1 = A[k][j + 5];
                  a2 = A[k][j + 6];
                  a3 = A[k][j + 7];
                  B[j + 4][k] = a0;
                  B[j + 5][k] = a1;
                  B[j + 6][k] = a2;
                  B[j + 7][k] = a3;
              }
          }
      }
  }
}

$ ./test-trans -M 64 -N 64

Function 0 (1 total)
Step 1: Validating and generating memory traces
Step 2: Evaluating performance (s=5, E=1, b=5)
func 0 (Transpose submission): hits:10754, misses:1027, evictions:995

Summary for official submission (func 0): correctness=1 misses=1027

TEST_TRANS_RESULTS=1:1027

61x67

本题2000miss,条件比较轻松,采用8x8分块和16x16分块应该都可以过

没什么优化的兴趣...

下附完整代码

void transpose_submit(int M, int N, int A[N][M], int B[M][N])
{
    if (M == 32) {
        int i, j, k, l;
        int t0, t1, t2, t3, t4, t5, t6, t7;
        for (i = 0; i < N; i += 8) {
            for (j = 0; j < M; j += 8) {
                if (i != j) {
                    for (k = i; k < i + 8; k++) {
                        for (l = j; l < j + 8; l++) {
                            B[l][k] = A[k][l];
                        }
                    }
                } else {
                    for (k = i; k < i + 8; k++) {
                        t0 = A[k][j];
                        t1 = A[k][j + 1];
                        t2 = A[k][j + 2];
                        t3 = A[k][j + 3];
                        t4 = A[k][j + 4];
                        t5 = A[k][j + 5];
                        t6 = A[k][j + 6];
                        t7 = A[k][j + 7];
                        B[k][j] = t0;
                        B[k][j + 1] = t1;
                        B[k][j + 2] = t2;
                        B[k][j + 3] = t3;
                        B[k][j + 4] = t4;
                        B[k][j + 5] = t5;
                        B[k][j + 6] = t6;
                        B[k][j + 7] = t7;
                    }
                    for (k = i; k < i + 8; k++) {
                        for (l = j + (k - i + 1); l < j + 8; l++) {
                            if (k != l) {
                                t0 = B[k][l];
                                B[k][l] = B[l][k];
                                B[l][k] = t0;
                            }
                        }
                    }
                }
            }
        }
    } else if (M == 64) {
        int i, j, k, l;
        int a0, a1, a2, a3, a4, a5, a6, a7;
        // 优先处理对角线block
        for (j = 0; j < N; j += 8) {
            // 对于第一行的block,借用矩阵选择第一行第二个block
            // 其余都选择每一行的第一个block
            if (j == 0)
                i = 8;
            else
                i = 0;
            // 1. 将A矩阵下方4x8移动到借用矩阵位置 - 上半部分
            for (k = j; k < j + 4; ++k) {
                a0 = A[k + 4][j + 0];
                a1 = A[k + 4][j + 1];
                a2 = A[k + 4][j + 2];
                a3 = A[k + 4][j + 3];
                a4 = A[k + 4][j + 4];
                a5 = A[k + 4][j + 5];
                a6 = A[k + 4][j + 6];
                a7 = A[k + 4][j + 7];
                B[k][i + 0] = a0;
                B[k][i + 1] = a1;
                B[k][i + 2] = a2;
                B[k][i + 3] = a3;
                B[k][i + 4] = a4;
                B[k][i + 5] = a5;
                B[k][i + 6] = a6;
                B[k][i + 7] = a7;
            }
            // 2. 借用矩阵内部两个4x4转置
            for (k = 0; k < 4; ++k) {
                for (l = k + 1; l < 4; ++l) {
                    a0 = B[j + k][i + l];
                    B[j + k][i + l] = B[j + l][i + k];
                    B[j + l][i + k] = a0;
                    a0 = B[j + k][i + l + 4];
                    B[j + k][i + l + 4] = B[j + l][i + k + 4];
                    B[j + l][i + k + 4] = a0;
                }
            }
            // 3. 将A上方4x8移动到B上方
            for (k = j; k < j + 4; ++k) {
                a0 = A[k][j + 0];
                a1 = A[k][j + 1];
                a2 = A[k][j + 2];
                a3 = A[k][j + 3];
                a4 = A[k][j + 4];
                a5 = A[k][j + 5];
                a6 = A[k][j + 6];
                a7 = A[k][j + 7];
                B[k][j + 0] = a0;
                B[k][j + 1] = a1;
                B[k][j + 2] = a2;
                B[k][j + 3] = a3;
                B[k][j + 4] = a4;
                B[k][j + 5] = a5;
                B[k][j + 6] = a6;
                B[k][j + 7] = a7;
            }
            // 4. B矩阵上方两个4x4转置
            for (k = j; k < j + 4; ++k) {
                for (l = k + 1; l < j + 4; ++l) {
                    a0 = B[k][l];
                    B[k][l] = B[l][k];
                    B[l][k] = a0;
                    a0 = B[k][l + 4];
                    B[k][l + 4] = B[l][k + 4];
                    B[l][k + 4] = a0;
                }
            }
            // 5. B矩阵的右上和转置矩阵的左上交换
            for (k = 0; k < 4; ++k) {
                a0 = B[j + k][j + 4];
                a1 = B[j + k][j + 5];
                a2 = B[j + k][j + 6];
                a3 = B[j + k][j + 7];
                B[j + k][j + 4] = B[j + k][i + 0];
                B[j + k][j + 5] = B[j + k][i + 1];
                B[j + k][j + 6] = B[j + k][i + 2];
                B[j + k][j + 7] = B[j + k][i + 3];
                B[j + k][i + 0] = a0;
                B[j + k][i + 1] = a1;
                B[j + k][i + 2] = a2;
                B[j + k][i + 3] = a3;
            }
            // 6. 将借用矩阵移动到B矩阵下方
            for (k = 0; k < 4; ++k) {
                B[j + k + 4][j + 0] = B[j + k][i + 0];
                B[j + k + 4][j + 1] = B[j + k][i + 1];
                B[j + k + 4][j + 2] = B[j + k][i + 2];
                B[j + k + 4][j + 3] = B[j + k][i + 3];
                B[j + k + 4][j + 4] = B[j + k][i + 4];
                B[j + k + 4][j + 5] = B[j + k][i + 5];
                B[j + k + 4][j + 6] = B[j + k][i + 6];
                B[j + k + 4][j + 7] = B[j + k][i + 7];
            }
            // 处理非对角线block
            for (i = 0; i < M; i += 8) {
                if (i == j) {
                    continue;
                } else {
                    // 1. 将A矩阵上半部分移动到B上半部分
                    //    分为两块 分别转置
                    for (k = i; k < i + 4; ++k) {
                        a0 = A[k][j + 0];
                        a1 = A[k][j + 1];
                        a2 = A[k][j + 2];
                        a3 = A[k][j + 3];
                        a4 = A[k][j + 4];
                        a5 = A[k][j + 5];
                        a6 = A[k][j + 6];
                        a7 = A[k][j + 7];
                        B[j + 0][k] = a0;
                        B[j + 1][k] = a1;
                        B[j + 2][k] = a2;
                        B[j + 3][k] = a3;
                        B[j + 0][k + 4] = a4;
                        B[j + 1][k + 4] = a5;
                        B[j + 2][k + 4] = a6;
                        B[j + 3][k + 4] = a7;
                    }
                    // 2. B矩阵右上部分移动到B矩阵左下,转置
                    //    A矩阵左下部分移动到B矩阵右上,转置
                    for (l = j; l < j + 4; ++l) {
                        a0 = A[i + 4][l];
                        a1 = A[i + 5][l];
                        a2 = A[i + 6][l];
                        a3 = A[i + 7][l];
                        a4 = B[l][i + 4];
                        a5 = B[l][i + 5];
                        a6 = B[l][i + 6];
                        a7 = B[l][i + 7];
                        B[l][i + 4] = a0;
                        B[l][i + 5] = a1;
                        B[l][i + 6] = a2;
                        B[l][i + 7] = a3;
                        B[l + 4][i + 0] = a4;
                        B[l + 4][i + 1] = a5;
                        B[l + 4][i + 2] = a6;
                        B[l + 4][i + 3] = a7;
                    }
                    // 3. A矩阵右下部分移动到B矩阵右下,转置
                    for (k = i + 4; k < i + 8; ++k) {
                        a0 = A[k][j + 4];
                        a1 = A[k][j + 5];
                        a2 = A[k][j + 6];
                        a3 = A[k][j + 7];
                        B[j + 4][k] = a0;
                        B[j + 5][k] = a1;
                        B[j + 6][k] = a2;
                        B[j + 7][k] = a3;
                    }
                }
            }
        }
    } else {
        // M = 61 N = 67
        int i, j, t0, t1, t2, t3, t4, t5, t6, t7;
        int k = N / 8 * 8;
        int l = M / 8 * 8;
        for (j = 0; j < l; j += 8)
            for (i = 0; i < k; ++i) {
                t0 = A[i][j];
                t1 = A[i][j + 1];
                t2 = A[i][j + 2];
                t3 = A[i][j + 3];
                t4 = A[i][j + 4];
                t5 = A[i][j + 5];
                t6 = A[i][j + 6];
                t7 = A[i][j + 7];
                B[j][i] = t0;
                B[j + 1][i] = t1;
                B[j + 2][i] = t2;
                B[j + 3][i] = t3;
                B[j + 4][i] = t4;
                B[j + 5][i] = t5;
                B[j + 6][i] = t6;
                B[j + 7][i] = t7;
            }
        for (i = k; i < N; ++i)
            for (j = l; j < M; ++j) {
                t0 = A[i][j];
                B[j][i] = t0;
            }
        for (i = 0; i < N; ++i)
            for (j = l; j < M; ++j) {
                t0 = A[i][j];
                B[j][i] = t0;
            }
        for (i = k; i < N; ++i)
            for (j = 0; j < M; ++j) {
                t0 = A[i][j];
                B[j][i] = t0;
            }
    }
}